如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)Rt△ADE与Rt△BEC全等吗?请写出必要的推理过程;
(2)△CED是不是直角三角形?请说明理由;
(3)若已知AD=6,AB=14,请求出请求出△CED的面积.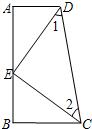
(本题满分8分) (1)计算:

(2)化简:

( 10分)如图,已知点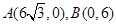 ,经过A、B的直线
,经过A、B的直线 以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线
以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线 上以每秒1个单位的速度沿直线
上以每秒1个单位的速度沿直线 向右下方向作匀速运动.设它们运动的时间为
向右下方向作匀速运动.设它们运动的时间为 秒.
秒.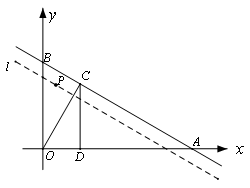
(1)用含
 的代数式表示点P的坐标;
的代数式表示点P的坐标;(2)过O作OC⊥AB于C,过C作CD⊥
 轴于D,问:
轴于D,问: 为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时
为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时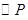 与直线CD的位置关系.
与直线CD的位置关系.
( 10分)保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2009年1 月的利润为200万元.设2009年1 月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2009年1 月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
⑴分别求该化工厂治污期间及治污改造工程完工后y与x之间对应的函数关系式.
⑵治污改造工程完工后经过几个月,该厂月利润才能达到2009年1月的水平?
⑶当月利润少于100万元时为该厂资金紧张期,问该厂资金紧张期共有几个月?
( 10分)如图, 是⊙O的直径,
是⊙O的直径, 为
为 延长线上的任意一点,
延长线上的任意一点,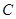 为半圆
为半圆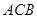 的中点,
的中点,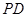 切⊙O于点
切⊙O于点 ,连结
,连结 交
交 于点
于点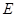 .
.
求证:(1)
 ;
;(2)
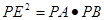 .
.
(8分)在东西方向的海岸线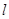 上有一长为1km的码头MN(如图),在码头西端M 的正西19.5 km 处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距
上有一长为1km的码头MN(如图),在码头西端M 的正西19.5 km 处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距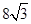 km的C处.
km的C处.
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.