已知函数 ,其中
,其中 。
。 。
。
(1)若 是函数
是函数 的极值点,求实数a的值;
的极值点,求实数a的值;
(2)若函数 的图象上任意一点处切线的斜率
的图象上任意一点处切线的斜率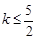 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若函数 在
在 上有两个零点,求实数a的取值范围.
上有两个零点,求实数a的取值范围.
已知椭圆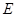 :
: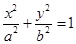 (
(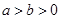 )过点
)过点 ,其左、右焦点分别为
,其左、右焦点分别为 ,且
,且 .
.
(1)求椭圆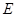 的方程;
的方程;
(2)若 是直线
是直线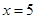 上的两个动点,且
上的两个动点,且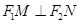 ,则以
,则以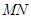 为直径的圆
为直径的圆 是否过定点?请说明理由.
是否过定点?请说明理由.
已知数列 满足:
满足: (其中常数
(其中常数 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)当 时,数列
时,数列 中是否存在不同的三项组成一个等比数列;若存在,求出满足条件的三项,若不存在,说明理由。
中是否存在不同的三项组成一个等比数列;若存在,求出满足条件的三项,若不存在,说明理由。
设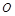 为正方形
为正方形 的中心,四边形
的中心,四边形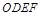 是平行四边形,且平面
是平行四边形,且平面 平面
平面 ,若
,若 .
.
(1)求证: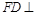 平面
平面 .
.
(2)线段 上是否存在一点
上是否存在一点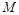 ,使
,使 平面
平面 ?若存在,求
?若存在,求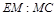 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.
(1)若该校高一年级共有学生 人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(2)若从数学成绩在 与
与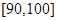 两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率。
两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率。
在 中,
中,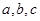 分别是角
分别是角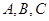 的对边,
的对边, ,
, .
.
(1)求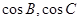 的值;
的值;
(2)若 ,求边
,求边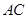 的长.
的长.