某公司有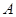 型产品40件,
型产品40件,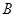 型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
| |
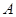 型利润 型利润 |
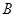 型利润 型利润 |
| 甲店 |
200 |
170 |
| 乙店 |
160 |
150 |
(1)设分配给甲店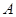 型产品
型产品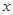 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为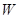 (元),求
(元),求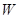 关于
关于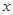 的函数关系式,并求出
的函数关系式,并求出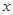 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,有多少种不同分配方案,哪种方案总利润最大,并求出最大值。
已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
(1)如图①,当直线l与⊙O 相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线l与⊙O 相交于点E、F时,若∠DAE=18°,求∠BAF的大小.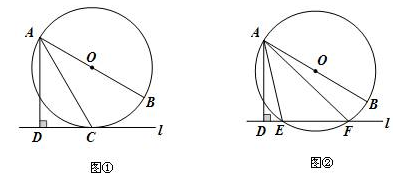
某文具店销售一种进价为每本10元的笔记本,为获得高利润,以不低于进价进行销售,结果发现,每月销售量y与销售单价x之间的关系可以近似地看作一次函数: ,物价部门规定这种笔记本每本的销售单价不得高于18元.
,物价部门规定这种笔记本每本的销售单价不得高于18元.
(1)当每月销售量为70本时,获得的利润为多少元;
(2)该文具店这种笔记本每月获得利润为w元,求每月获得的利润w元与销售单价x之间的函数关系式,并写出自变量的取值范围;
(3)当销售单价定为多少元时,每月可获得最大利润,最大利润为多少元?
如图,AB是⊙O的直径,点F,C是⊙O上两点,且 ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.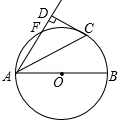
(1)求证:CD是⊙O的切线;
(2)若CD= ,求⊙O的半径.
,求⊙O的半径.
已知:y关于x的函数 的图象与x轴有交点.
的图象与x轴有交点.
(1)求k的取值范围;
(2)若 ,
, 是函数图象与x轴两个交点的横坐标,且满足
是函数图象与x轴两个交点的横坐标,且满足 .
.
①求k的值;
②当k≤x≤k+2时,请结合函数图象确定y的最大值和最小值.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
(1)将△ABC绕点B顺时针旋转90°得到△A′BC′,请画出△A′BC′;
(2)求BA边旋转到B A′位置时所扫过图形的面积.