已知椭圆 :
: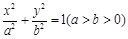 的离心率为
的离心率为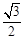 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线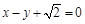 相切.
相切.
(1)求椭圆C的方程;
(2)设 ,
,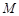 、
、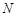 是椭圆
是椭圆 上关于
上关于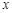 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结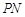 交椭圆
交椭圆 于另一点
于另一点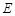 ,求直线
,求直线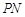 的斜率的取值范围;
的斜率的取值范围;
(3)在(2)的条件下,证明直线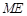 与
与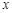 轴相交于定点.
轴相交于定点.
已知函数 .
.
(1)设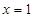 是函数
是函数 的极值点,求
的极值点,求 的值并讨论
的值并讨论 的单调性;
的单调性;
(2)当 时,证明:
时,证明: >
> .
.
已知椭圆 :
: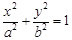 (
( )的焦距为
)的焦距为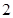 ,且过点(
,且过点( ,
, ),右焦点为
),右焦点为 .设
.设 ,
, 是
是 上的两个动点,线段
上的两个动点,线段 的中点
的中点 的横坐标为
的横坐标为 ,线段
,线段 的中垂线交椭圆
的中垂线交椭圆 于
于 ,
, 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)求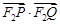 的取值范围.
的取值范围.
若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”.已知数列
为“平方递推数列”.已知数列 中,
中, ,点
,点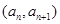 在函数
在函数 的图象上,其中
的图象上,其中 为正整数.
为正整数.
(1)证明数列 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列;
为等比数列;
(2)设(1)中“平方递推数列”的前 项积为
项积为 ,
,
即 ,求
,求 ;
;
(3)在(2)的条件下,记 ,求数列
,求数列 的前
的前 项和
项和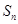 ,并求使
,并求使 的
的 的最小值.
的最小值.
中国男子篮球职业联赛总决赛采用七场四胜制(即先胜四场者获胜).进入总决赛的甲乙两队中,若每一场比赛甲队获胜的概率为 ,乙队获胜的概率为
,乙队获胜的概率为 ,假设每场比赛的结果互相独立.现已赛完两场,乙队以
,假设每场比赛的结果互相独立.现已赛完两场,乙队以 暂时领先.
暂时领先.
(1)求甲队获得这次比赛胜利的概率;
(2)设比赛结束时两队比赛的场数为随机变量 ,求随机变量
,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
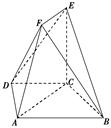
在如图所示的几何体中,四边形 是等腰梯形,
是等腰梯形, ∥
∥ ,
, ,
, .在梯形
.在梯形 中,
中, ∥
∥ ,且
,且 ,
, ⊥平面
⊥平面 .
.
(1)求证: ;
;
(2)若二面角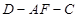 为
为 ,求
,求 的长.
的长.