已知正四棱柱ABCD—A1B1C1D1的底面边长AB=6，侧棱长
，它的外接球的球心为O，点E是AB的中点，点P是球O的球面上任意一点，则有以下结论：
①PE长的最大值是9；
②三棱锥P—EBC的最大值是
[]
③存在过点E的平面，截球O的截面面积是
；
④三棱锥P—AEC1体积的最大值是20。
其中正确结论的是 。（写出所有正确结论的序号）
设抛物线y2＝8x的准线与x轴交于点Q，若过点Q的直线l与抛物线有公共点，则直线l的斜率的取值范围是________．
已知椭圆C：
＝1(a>b>0)的离心率为
，与过右焦点F且斜率为k(k>0)的直线相交于A、B两点．若
＝3
，则k＝________．
已知双曲线E的中心为原点，F(3，0)是E的焦点，过F的直线l与E相交于A、B两点，且AB的中点为N(－12，－15)，则E的方程为____________．
若斜率为
的直线l与椭圆
＝1(a>b>0)有两个不同的交点，且这两个交点在x轴上的射影恰好是椭圆的两个焦点，则该椭圆的离心率为________．
已知双曲线方程是x2－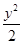
＝1，过定点P(2，1)作直线交双曲线于P1、P2两点，并使P(2，1)为P1P2的中点，则此直线方程是____________．