某班在联欢会上举行一个抽奖活动,甲箱中有3个红球,2个黑球,乙箱中装有2个红球4个黑球,参加活动者从这两个箱子中分别摸出1个球,如果摸到的都是红球则获奖.
(Ⅰ)求每个活动参加者获奖的概率;
(Ⅱ)某办公室共有5人,每人抽奖1次,求这5人中至少有3人获奖的概率.
已知A(-2,4),B(3,-1),C(-3,-4).
设 =a,
=a,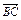 =b,
=b,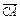 =c,且
=c,且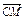 =3c,
=3c,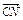 =-2b,
=-2b,
(1)求:3a+b-3c;
(2)求满足a=mb+nc的实数m,n.
如图所示,在平行四边形ABCD中,M,N分别为DC,BC的中点,已知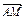 =c,
=c,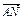 =d,试用c,d表示
=d,试用c,d表示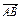 ,
,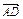 .
.
已知点A(1,0)、B(0,2)、C(-1,-2),求以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
设两个非零向量e1和e2不共线.
(1)如果 =e1-e2,
=e1-e2, =3e1+2e2,
=3e1+2e2,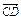 =-8e1-2e2,
=-8e1-2e2,
求证:A、C、D三点共线;
(2)如果 =e1+e2,
=e1+e2, =2e1-3e2,
=2e1-3e2,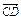 =2e1-ke2,且A、C、D三点共线,求k的值.
=2e1-ke2,且A、C、D三点共线,求k的值.
已知点G为△ABC的重心,过G作直线与AB、AC两边分别交于M、N两点,且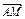 =x
=x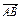 ,
, =y
=y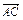 ,求
,求 +
+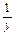 的值.
的值.