已知向量m=(cosx,sinx),n=(cosx,cosx)(x∈R),设函数f(x)=m·n
(1)求 f(x)的解析式,并求最小正周期.
(2)若函数 g(x)的图像是由函数 f(x)的图像向右平移 个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.
个单位得到的,求g(x)的最大值及使g(x)取得最大值时x的值.
(本小题共14分)如图,四棱锥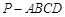 的底面是直角梯形,
的底面是直角梯形,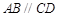 ,
,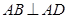 ,
, 和
和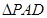 是两个边长为
是两个边长为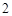 的正三角形,
的正三角形,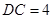 ,
,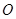 为
为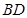 的中点,
的中点,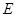 为
为 的中点.
的中点.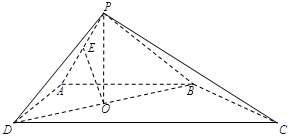
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: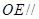 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题共13分)某商场一号电梯从1层出发后可以在2、3、4层停靠.已知该电梯在1层载有4位乘客,假设每位乘客在2、3、4层下电梯是等可能的.
(Ⅰ) 求这4位乘客中至少有一名乘客在第2层下电梯的概率;
(Ⅱ) 用 表示4名乘客在第4层下电梯的人数,求
表示4名乘客在第4层下电梯的人数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题共13分)已知函数
 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 的单调区间及其图象的对称轴方程.
的单调区间及其图象的对称轴方程.
(本小题满分13分)已知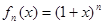 ,
,
(Ⅰ)若 ,求
,求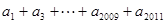 的值;
的值;
(Ⅱ)若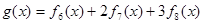 ,求
,求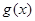 中含
中含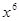 项的系数;
项的系数;
(Ⅲ)证明: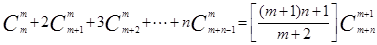
(本小题满分13分)如图:平行四边形 的周长为8,点
的周长为8,点 的坐标分别为
的坐标分别为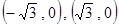 .
.
(Ⅰ)求点 所在的曲线方程;
所在的曲线方程;
(Ⅱ)过点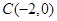 的直线
的直线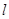 与(Ⅰ)中曲线交于点
与(Ⅰ)中曲线交于点 ,与y轴交于点
,与y轴交于点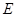 ,且
,且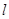 //
// ,求证:
,求证: 为定值.
为定值.