在直角坐标系 中,以原点
中,以原点 为极点,以
为极点,以 轴非负半轴为极轴,与直角坐标系
轴非负半轴为极轴,与直角坐标系 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线 参数方程为
参数方程为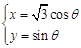 (
(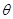 为参数),直线
为参数),直线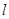 的极坐标方程为
的极坐标方程为 .
.
(1)写出曲线 的普通方程和直线
的普通方程和直线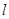 的直角坐标方程;
的直角坐标方程;
(2)求曲线 上的点到直线
上的点到直线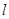 的最大距离.
的最大距离.
两人相约在7点到8点在某地会面,先到者等候另一个人20分钟方可离去. 试求这两人能会面的概率?
袋里装有35个球,每个球上都标有从1到35的一个号码,设号码n的球重 (克).这些球以等可能性(不受重量的影响)从袋里取出.
(克).这些球以等可能性(不受重量的影响)从袋里取出.
(1)如果任意取出一球,试求其重量大于号码数的概率;
(2)如果同时任意取出二球,试求它们重量相同的概率.
用下图所示的转盘进行配紫色(红色与蓝色配成)游戏:其中A转盘蓝色部分占整个转盘的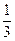 .求游戏者获胜的概率?
.求游戏者获胜的概率?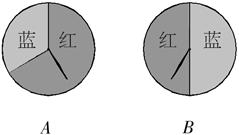
袋中有1个白球,2个黄球,问
(1)从中一次性地随机摸出2个球,都是黄球的概率是多少?
(2)先从中摸出一球,再从剩下的球中摸出一球,两次都是黄球的概率是多少?
(3)先从中摸出一球,将它放回口袋中后,再摸一次,两次都是黄球的概率是多少?
质地均匀的三个几何体A、B、C. A是硬币,正面涂红色,反面涂黄色;B是正四面体涂了红黄蓝白四色,每面一色;C是正方体,每面涂一色,涂有红黄蓝三色,每种颜色两个面,在水平地面上依次投A、B、C各一次,几何体与地面接触的面的颜色称为“保留色”。
(1)求A、B、C的“保留色”相同的概率;
(2)求A、B、C的“保留色”恰为两个红色的概率;
(3)求A、B、C的“保留色”互不相同的概率;