（本题满分14分
已知椭圆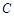
：
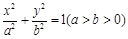的离心率为
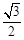，以原点为圆心，
椭圆的短半轴长为半径的圆与直线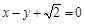
相切．
⑴求椭圆C的方程；
⑵设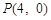
，
、
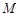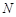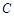是椭圆上关于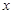
轴对称的任意两个不同的点，连结
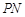交椭圆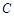
于另一点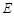
，求直线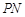的斜率的取值范围；
⑶在⑵的条件下，证明直线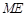
与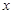轴相交于定点．
在直角坐标平面内，将每个点绕原点按逆时针方向旋转
的变换
所对应的矩阵为
,将每个点横、纵坐标分别变为原来的
倍的变换
所对应的矩阵为
．
（1）求矩阵的逆矩阵
；
（2）求曲线
先在变换作用下，然后在变换作用下得到的曲线方程．
设
(
是自然对数的底数，
)，且
．
（1）求实数
的值，并求函数
的单调区间；
（2）设
，对任意
，恒有
成立．求实数
的取值范围；
（3）若正实数
满足
，
，试证明：
；并进一步判断：当正实数
满足
，且
是互不相等的实数时，不等式
是否仍然成立．
如图所示，在边长为
的正方形
中，点
在线段
上，且
，
，作
//
，分别交
，
于点
，
，作
//，分别交，于点
，
，将该正方形沿，折叠，使得
与重合，构成如图所示的三棱柱
．
（1）求证：
平面
；
（2）若点E为四边形BCQP内一动点,且二面角E-AP-Q的余弦值为
,求|BE|的最小值.
如图，在圆
上任取一点
，过点作
轴的垂线段
，
为垂足．设
为线段的中点．
（1）当点在圆
上运动时，求点的轨迹
的方程；
（2）若圆在点处的切线与轴交于点
，试判断直线
与轨迹的位置关系．
已知函数
（
,
,
）,
的部分图像如图所示,
、
分别为该图像的最高点和最低点,点的坐标为
．
（1）求
的最小正周期及
的值；
（2）若点
的坐标为
,
,求
的值和
的面积．