如图，等边三角形OAB的边长为2，将线段OB绕着点O逆时针旋转60°得到线段OC,连结BC。
（1）试判定四边形OABC的形状；
（2）求点O到BC的距离；
（3）以O为圆心，r为半径作⊙O，根据⊙O与四边形OABC四条边交点的总个数，求相应r的取值范围。
三个队植树，第一个队植树x棵，第二个队比第一个队植的树2倍还多8棵，第三队植的树比第二队的一半少6棵，问三个队共植树多少棵？并求当x=100时，三个队共植树多少棵？
一小虫从某点O出发在一天直线上来回爬行，假定向右爬行的路程记为正数，向左爬行的路程记为负数，爬过的各段路程依次为：（单位：厘米） +2，-6，-6，+12，-10，+11，-3
（1）小虫最后是否回到出发点O呢？
小虫离开出发点O最远是多少厘米？
在爬行过程中，如果每爬行1厘米奖励三支铅笔，那么小虫一共得到了多少支铅笔呢？
（本题8分）如图，在平面直角坐标系中，O是坐标原点，点A坐标为（2，0），点B坐标为（0，b）（b＞0），点P是直线AB上位于第二象限内的一个动点，过点P作PC垂直于x轴于点C，记点P关于y轴的对称点为Q，设点P的横坐标为a．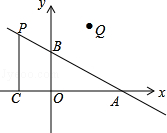
（1）当b=3时：①求直线AB相应的函数表达式；②当S△QOA=4时，求点P的坐标；
（2）是否同时存在a、b，使得△QAC是等腰直角三角形？若存在，求出所有满足条件的a、b的值；若不存在，请说明理由．
（本题10分）如图，在平面直角坐标系中，直线
＋2与x轴、y轴分别交于A、B两点，以AB为边在第二象限内作正方形ABCD．
（1）求点A、B的坐标，并求边AB的长；
（2）求点D和点C的坐标；
（3）你能否在x轴上找一点M，使△MDB的周长最小?如果能，请求出M点的坐标；如果不能，说明理由．
（本题8分）为了发展旅游经济，我市某景区采用灵活的售票方法吸引游客．门票定价为50元/人，非节假日打a折售票，节假日按团队人数分段定价售票，即m人以下（含m人）的团队按原价售票；超过m人的团队，其中m人仍按原价售票，超过m人部分的游客打b折售票．设某旅游团人数为x人，非节假日购票金额为y1（元），节假日购票金额为y2（元）．y1、y2与x之间的函数关系如图所示．
（1）观察图象可知：a＝_______；b＝_______；m＝_______．
（2）直接写出y1、y2与x之间的函数关系式．
（3）某旅行社导游王娜于5月1日带A团，5月20日（非节假日）带B团都到该景区旅游，共付门票款1900元，A、B两个团队合计50人，A、B两个团队各有多少人？