(本题8分)为了发展旅游经济,我市某景区采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票金额为y1(元),节假日购票金额为y2(元).y1、y2与x之间的函数关系如图所示.
(1)观察图象可知:a=_______;b=_______;m=_______.
(2)直接写出y1、y2与x之间的函数关系式.
(3)某旅行社导游王娜于5月1日带A团,5月20日(非节假日)带B团都到该景区旅游,共付门票款1900元,A、B两个团队合计50人,A、B两个团队各有多少人?
如图,在Rt△ABC中,∠C为直角,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
若AC=8,AB=12,求⊙O的半径;
连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由
如图,∠C=90º,点A、B在∠C的两边上,CA=30,CB=20,连接AB.点P从点B出发,以每秒4个单位长度的速度沿BC的方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于点D,作DE⊥AC于点E.F为射线CB上一点,使得∠CEF=∠ABC.设点P运动的时间为x秒.用含有x的代数式表示CE的长
求点F与点B重合时x的值
当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式

如图,在平面直角坐标系 中,抛物线
中,抛物线 与
与 轴交于点
轴交于点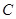 ,与
,与 轴交于
轴交于 两点,直线
两点,直线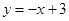 恰好经过
恰好经过 两点.
两点.求出抛物线
 的解析式,并写出抛物线的对称轴;
的解析式,并写出抛物线的对称轴;点
 在抛物线的对称轴上,抛物线顶点为D若
在抛物线的对称轴上,抛物线顶点为D若 ,求点
,求点 的坐标.
的坐标.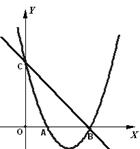
如图,⊙O的直径AB=8,C为圆周上一点,AC=4,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点E.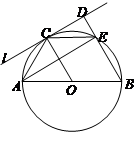
求∠AEC的度数
求证:四边形OBEC是菱形
某小区准备新建50个停车位,以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位需0.5万元;新建3个地上停车位和2个地下停车位需1.1万元.该小区新建1个地上停车位和1个地下停车位各需多少万元?
若该小区预计投资金额超过10万元而不超过11万元,则共有几种建造方案?