如图，⊙O的直径AB=8，C为圆周上一点，AC=4，过点C作⊙O的切线l，过点B作l的垂线BD，垂足为D，BD与⊙O交于点E．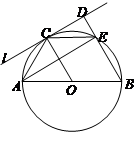
求∠AEC的度数
求证：四边形OBEC是菱形
计算：(每小题8分，共16分)(1) ×÷
(2) ＋6－2x
（本小题满分14分）
如图①，已知四边形ABCD是正方形，点E是AB的中点，点F在边CB的延长线上，且BE=BF，连接EF．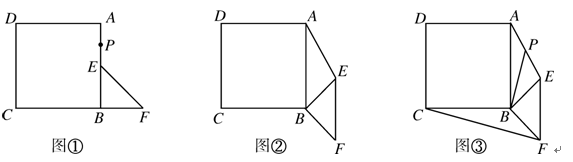
（1）若取AE的中点P，求证：BP=
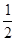CF；（2）在图①中，若将
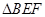绕点B顺时针方向旋转
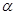（00<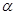<3600），如图②，是否存在某位置，使得
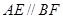？，若存在，求出所有可能的旋转角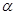的大小；若不存在，请说明理由；（3）在图①中，若将△BEF绕点B顺时针旋转
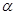（00<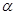<900），如图③，取AE的中点P，连接BP、CF，求证：BP=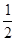CF且BP⊥CF．
（本小题满分14分）
如图所示，抛物线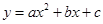
经过原点
，与
轴交于另一点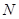
,直线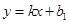
与两坐标轴分别交于
、
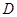两点，与抛物线交于
、
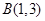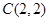两点.
（1）求直线与抛物线的解析式；
（2）若抛物线在
轴上方的部分有一动点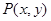
，
求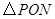
的面积最大值；（3）若动点
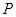保持（2）中的运动路线，问是否存在点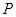，使得
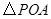的面积等于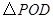
面积的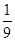
？若存在，请求出点的坐标；
若不存在，请说明理由．
（本小题满分12分）
如图，AB、BC、CD分别与⊙O切于E、F、G，且AB∥CD．连接OB、OC，延长CO交⊙O于点M，过点M作MN ∥OB交CD于N．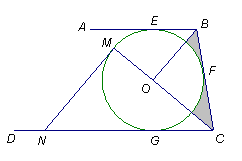
⑴求证：MN是⊙O的切线；
⑵当0B=6cm，OC=8cm时，求⊙O的半径及图中阴影部分的面积．
（本小题满分12分）
甲、乙、丙三个人准备打羽毛球，他们约定用“抛硬币”的方式来确定哪两个人先上场，三人手中各持有一枚质地均匀的硬币，同时将手中硬币抛落到水平地面为一个回合．落地后，三枚硬币中，恰有两枚正面向上或反面向上的这两枚硬币持有人先上场；若三枚硬币均为正面向上或反面向上，属于不能确定．（1）请你画出表示“抛硬币”一个回合所有可能出现的结果的树状图；
（2）求一个回合能确定两人先上场的概率．