在平面直角坐标系 中,已知点
中,已知点
 ,点P是动点,且三角形
,点P是动点,且三角形 的三边所在直线
的三边所在直线
的斜率满足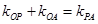 .
.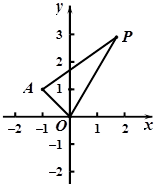
(1)求点P的轨迹 的方程;
的方程;
(2)设Q是轨迹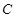 上异于点
上异于点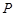 的一个点,若
的一个点,若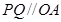 ,直线
,直线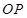 与
与 交于点M,探究是否存点P使得
交于点M,探究是否存点P使得 和
和 的面积满足
的面积满足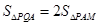 ,若存在,求出点P的坐标;若不存在,说明理由.
,若存在,求出点P的坐标;若不存在,说明理由.
如图,在四棱锥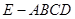 中,四边形
中,四边形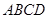 为平行四边形,
为平行四边形, 为
为 上一点,且
上一点,且 .
.
(1)求证: ;
;
(2)若点 为线段
为线段 的中点,求证:
的中点,求证: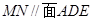 ;
;
(3) 若 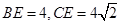 ,且二面角
,且二面角 的大小为
的大小为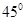 ,
,
求三棱锥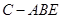 的体积.
的体积.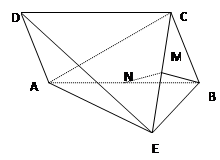
在 中
中 分别为角
分别为角 所对的边的边长,
所对的边的边长,
(1)试叙述正弦或余弦定理并证明之;
(2)设 ,求证:
,求证: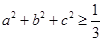 .
.
一笼子中装有2只白猫,3只黑猫,笼门打开每次出来一只猫,每次每只猫都有可能出来.
(1)第三次出来的是只白猫的概率;
(2)记白猫出来完时笼中所剩黑猫数为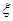 ,试求
,试求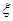 的概率分布列及期望.
的概率分布列及期望.
设函数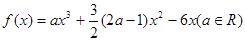
(1)当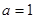 时,求曲线
时,求曲线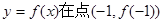 处的切线方程;
处的切线方程;
(2)当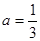 时,求
时,求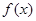 的极大值和极小值;
的极大值和极小值;
(3)若函数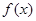 在区间
在区间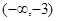 上是增函数,求实数
上是增函数,求实数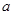 的取值范围.
的取值范围.
已知椭圆的长轴长为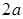 ,焦点是
,焦点是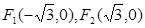 ,点
,点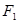 到直线
到直线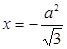 的距离为
的距离为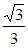 ,过点
,过点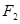 且倾斜角为锐角的直线
且倾斜角为锐角的直线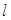 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得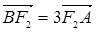 .
.
(1)求椭圆的标准方程; (2)求直线l的方程.