(本小题满分12分)
设函数
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)当 时,设
时,设 的最小值为
的最小值为 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
设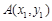 、
、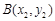 是函数
是函数 图象上任意两点,且
图象上任意两点,且 .
.
(1)求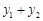 的值;
的值;
(2)若 …
…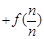 (其中
(其中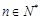 ),求
),求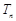 ;
;
(3)在(2)的条件下,设 (
(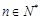 ),若不等式
),若不等式 …
…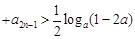 对任意的正整数n恒成立,求实数a的取值范围.
对任意的正整数n恒成立,求实数a的取值范围.
已知几何体 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.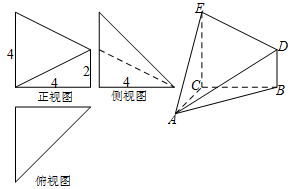
(1)求此几何体的体积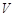 的大小;
的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)求二面角A-ED-B的正弦值.
设公差不为0的等差数列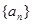 的首项为1,且
的首项为1,且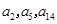 构成等比数列.
构成等比数列.
(1)求数列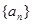 的通项公式;
的通项公式;
(2)若数列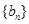 满足
满足 …
… 1-
1- ,n∈N*,求
,n∈N*,求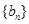 的前n项和
的前n项和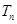 .
.
某运输公司有12名驾驶员和19名工人,有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车.某天需运往 地至少72吨的货物,派用的每辆车须满载且只运送一次.派用的每吨甲型卡车须配2名工人,运送一次可得利润450元;派用的每辆乙型卡车须配1名工人,运送一次可得利润350元.问该公司如何派用两类卡车的车辆数可得最大利润?
地至少72吨的货物,派用的每辆车须满载且只运送一次.派用的每吨甲型卡车须配2名工人,运送一次可得利润450元;派用的每辆乙型卡车须配1名工人,运送一次可得利润350元.问该公司如何派用两类卡车的车辆数可得最大利润?
已知△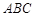 的三个内角
的三个内角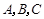 所对的边分别为a,b,c,向量
所对的边分别为a,b,c,向量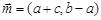 ,
, ,且
,且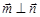 .
.
(1)求角 的大小;
的大小;
(2)若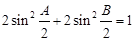 ,判断△
,判断△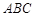 的形状.
的形状.