在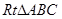 中,
中,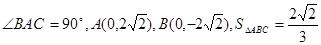 ,动点P的轨迹为曲线E,曲线E过点C且满足|PA|+|PB|为常数。
,动点P的轨迹为曲线E,曲线E过点C且满足|PA|+|PB|为常数。
(1)求曲线E的方程;
(2)是否存在直线L,使L与曲线E交于不同的两点M、N,且线段MN恰被直线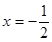 平分?若存在,求出L的斜率的取值范围;若不存在说明理由。
平分?若存在,求出L的斜率的取值范围;若不存在说明理由。
已知圆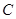 :
: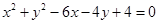 ,直线
,直线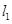 被圆所截得的弦的中点为P(5,3).(1)求直线
被圆所截得的弦的中点为P(5,3).(1)求直线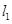 的方程;(2)若直线
的方程;(2)若直线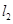 :
: 与圆
与圆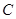 相交于两个不同的点,求b的取值范围.
相交于两个不同的点,求b的取值范围.
已知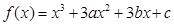 在
在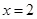 处有极值,其图象在
处有极值,其图象在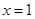 处的切线与直线
处的切线与直线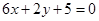 平行.
平行.
(1)求函数的单调区间;
(2)若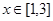 时,
时, 恒成立,求实数
恒成立,求实数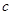 的取值范围。
的取值范围。
已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为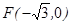 ,且过
,且过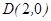 ,设点
,设点 .
.
(1)求该椭圆的标准方程;
(2)若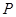 是椭圆上的动点,求线段
是椭圆上的动点,求线段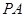 中点
中点 的轨迹方程。
的轨迹方程。
(本小题满分8分) 某车间生产某机器的两种配件A和B,生产配件A成本费y 与该车间的工人人数x成反比,而生产配件B成本费y
与该车间的工人人数x成反比,而生产配件B成本费y 与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y
与该车间的工人人数x成正比,如果该车间的工人人数为10人时,这两项费用y 和y
和y 分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?
分别为2万元和8万元,那么要使这两项费用之和最小,该车间的工人人数x应为多少?
如图,P—ABCD是正四棱锥,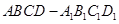 是正方体,其中
是正方体,其中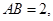


(1)求证: ;
;
(2)求平面PAD与平面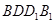 所成的锐二面角
所成的锐二面角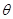 的余弦值;
的余弦值;