(本小题满分14分)
已知函数 ,(
,( e为自然对数的底数)
e为自然对数的底数)
(Ⅰ)当a=1时,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在 上无零点,求a的最小值;
上无零点,求a的最小值;
(III)若对任意给定的 ,在
,在 上总存在两个不同的
上总存在两个不同的 ,使得
,使得 成立,求a的取值范围.
成立,求a的取值范围.
(本小题满分7分)《选修4-4:坐标系与参数方程》
已知直线的极坐标方程为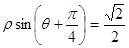 ,圆
,圆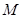 的参数方程为
的参数方程为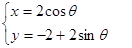 (其中
(其中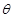 为参数).
为参数).
(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)求圆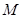 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.
(本小题满分7分)选修4—2:矩阵与变换
如图,矩形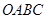 的
的 在变换
在变换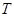 的作用下分别变成
的作用下分别变成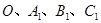 ,形成了平行四边形
,形成了平行四边形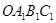
(Ⅰ)求变换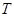 对应的矩阵
对应的矩阵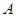 ;
;
(Ⅱ)变换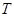 对应的矩阵
对应的矩阵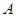 将直线
将直线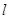 变成了直线
变成了直线 :
: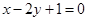 ,求直线
,求直线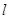 的(1)方程.
的(1)方程.
设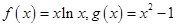 .
.
(1)令 ,求
,求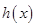 的单调区间;
的单调区间;
(2)若当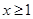 时,
时,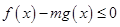 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
已知椭圆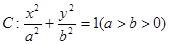 经过点
经过点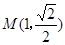 ,其离心率为
,其离心率为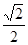 ,设直线
,设直线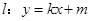 与椭圆
与椭圆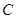 相交于
相交于 两点.
两点.
(Ⅰ)求椭圆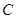 的方程;
的方程;
(Ⅱ)已知直线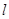 与圆
与圆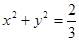 相切,求证:
相切,求证: (
( 为坐标原点);
为坐标原点);
(Ⅲ)以线段 为邻边作平行四边形
为邻边作平行四边形 ,若点
,若点 在椭圆
在椭圆 上,且满足
上,且满足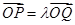 (
(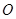 为坐标原点),求实数
为坐标原点),求实数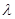 的取值范围.
的取值范围.
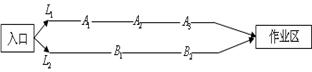
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有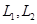 两条巷道通往作业区(如下图),
两条巷道通往作业区(如下图), 巷道有
巷道有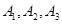 三个易堵塞点,各点被堵塞的概率都是
三个易堵塞点,各点被堵塞的概率都是 ;
;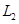 巷道有
巷道有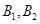 两个易堵塞点,被堵塞的概率分别为
两个易堵塞点,被堵塞的概率分别为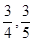 .
.
(1)求 巷道中,三个易堵塞点最多有一个被堵塞的概率;
巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若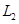 巷道中堵塞点个数为
巷道中堵塞点个数为 ,求
,求 的分布列及数学期望
的分布列及数学期望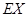 ,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.