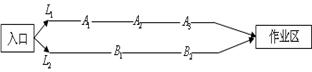
某煤矿发生透水事故时,作业区有若干人员被困.救援队从入口进入之后有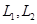 两条巷道通往作业区(如下图),
两条巷道通往作业区(如下图), 巷道有
巷道有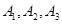 三个易堵塞点,各点被堵塞的概率都是
三个易堵塞点,各点被堵塞的概率都是 ;
;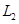 巷道有
巷道有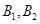 两个易堵塞点,被堵塞的概率分别为
两个易堵塞点,被堵塞的概率分别为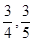 .
.
(1)求 巷道中,三个易堵塞点最多有一个被堵塞的概率;
巷道中,三个易堵塞点最多有一个被堵塞的概率;
(2)若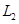 巷道中堵塞点个数为
巷道中堵塞点个数为 ,求
,求 的分布列及数学期望
的分布列及数学期望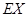 ,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
已知函数 ,其中
,其中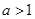 .
.
(1)判断并证明函数 的奇偶性;
的奇偶性;
(2)判断并证明函数 的单调性.
的单调性.
已知集合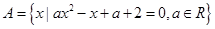 .
.
(1)若 中只有一个元素,求
中只有一个元素,求 的值,并把这个元素写出来;
的值,并把这个元素写出来;
(2)若 中至多只有一个元素,求
中至多只有一个元素,求 的取值范围.
的取值范围.
(1)计算: ;
;
(2)设 ,求
,求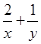 的值.
的值.
设函数 .
.
(1)若函数 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.
设双曲线C: (a>0,b>0)的一个焦点坐标为(
(a>0,b>0)的一个焦点坐标为( ,0),离心率
,0),离心率 , A、B是双曲线上的两点,AB的中点M(1,2).
, A、B是双曲线上的两点,AB的中点M(1,2).
(1)求双曲线C的方程;
(2)求直线AB方程;
(3)如果线段AB的垂直平分线与双曲线交于C、D两点,那么A、B、C、D四点是否共圆?为什么?