如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,∠BAD=60°.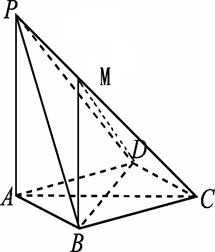
(Ⅰ)求证:直线BD⊥平面PAC;
(Ⅱ)求直线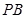 与平面
与平面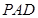 所成角的正切值;
所成角的正切值;
(Ⅲ)已知M在线段PC上,且BM=DM=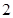 ,CM=3,求二面角
,CM=3,求二面角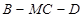 的余弦值.
的余弦值.
(本小题满分16分)已知数列
 ,其中数列
,其中数列 是首项为2公比为
是首项为2公比为 的等比数列,又
的等比数列,又 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求使不等式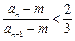 成立的所有正整数
成立的所有正整数 的值.
的值.
(本小题满分16分)
已知函数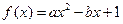 ,
,
(Ⅰ)是否存在实数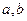 使
使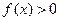 的解集是
的解集是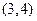 ,若存在,求实数
,若存在,求实数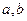 的值,若不存在请说明理由.
的值,若不存在请说明理由.
(Ⅱ)若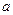
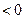 ,
, ,且不等式
,且不等式 在
在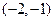 上恒成立,求
上恒成立,求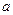 的取值范围.
的取值范围.
(本小题满分15分)数列 的前
的前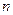 项和为
项和为 ,
, ,
,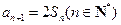 .
.
(Ⅰ)求数列 的通项
的通项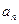 ;(Ⅱ)求数列
;(Ⅱ)求数列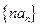 的前
的前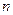 项和
项和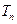 .
.
(本小题满分15分)
如图,某单位用木料制作如图所示的框架,框架的下部是边长分别为 (单位:米)的矩形,上部是斜边长为
(单位:米)的矩形,上部是斜边长为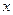 的等腰直角三角形,要求框架围成的总面积为8平方米.
的等腰直角三角形,要求框架围成的总面积为8平方米.
(Ⅰ)求 的关系式,并求
的关系式,并求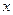 的取值范围;
的取值范围;
(Ⅱ)问 分别为多少时用料最省?
分别为多少时用料最省?
(本小题满分14分)
在ΔABC中,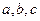 分别为
分别为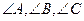 的对边,已知
的对边,已知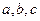 成等比数列,且
成等比数列,且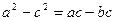 .求:
.求:
(Ⅰ)A的大小; (Ⅱ)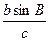 的值.
的值.