(本小题满分12分)在我校值周活动中,甲、乙等五名值周生被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名值周生.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量X为这五名值周生中参加A岗位服务的人数,求X的分布列及期望.
已知数列 满足
满足 =-1,
=-1, ,数列
,数列 满足
满足
(1)求证:数列 为等比数列,并求数列
为等比数列,并求数列 的通项公式.
的通项公式.
(2)求证:当 时,
时,
(3)设数列 的前
的前 项和为
项和为 ,求证:当
,求证:当 时,
时, .
.
已知圆C: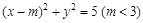 过点A(3,1),且过点P(4,4)的直线PF与圆C相切并和x轴的负半轴相交于点F.
过点A(3,1),且过点P(4,4)的直线PF与圆C相切并和x轴的负半轴相交于点F.
(1)求切线PF的方程;
(2)若抛物线E的焦点为F,顶点在原点,求抛物线E的方程.
(3)若Q为抛物线E上的一个动点,求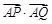 的取值范围.
的取值范围.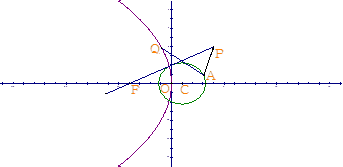
已知函数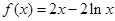
(Ⅰ)求函数在(1,  )的切线方程
)的切线方程
(Ⅱ)求函数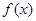 的极值
的极值
(Ⅲ)对于曲线上的不同两点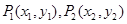 ,如果存在曲线上的点
,如果存在曲线上的点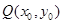 ,且
,且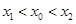 ,使得曲线在点
,使得曲线在点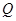 处的切线
处的切线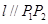 ,则称
,则称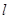 为弦
为弦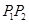 的陪伴切线.
的陪伴切线.
已知两点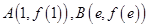 ,试求弦
,试求弦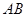 的陪伴切线
的陪伴切线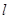 的方程;
的方程;
一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取一个,求:
(Ⅰ)连续取两次都是白球的概率;
(Ⅱ)若取一个红球记2分,取一个白球记1分,取一个黑球记0 分,连续取三次分数之和为4分的概率.
已知四棱锥 底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F
底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F
分别是线段AB.BC的中点,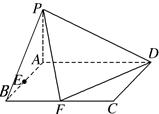
(1)证明:PF⊥FD;
(2)在PA上找一点G,使得EG∥平面PFD;.
(3)若 与平面
与平面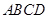 所成的角为
所成的角为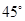 ,求二面角
,求二面角 的余弦值.
的余弦值.