已知代数式x+2y的值是3,则代数式2x+4y+1值是 .
如图,在ΔABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.(1)当x为何值时,PQ∥BC?(2)当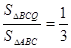 ,求
,求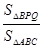 的值;
的值;
已知:如图,∠ABE=90°,且AB=BC=CD=DE,请认真研究图形与所给条件,然后回答:图中是否存在相似的三角形?若存在,请加以说明;若不存在,请说明理由.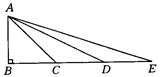
如图,是利用木杆撬石头的示意图.现有一块石头,要使其滚动,杠杆的B端必须向上翘起12cm,已知杠杆的动力臂OA与阻力臂OB之比为5:1,求要使这块石头滚动,至少要将杠杆A端下压多少厘米.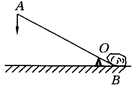
如图,已知△ABC中,AC=10,AB=16,问在AB边上是否存在这样的点P,使△APC∽△ACB,若存在,求AP的长;若不存在,请说明理由.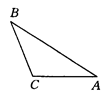
如图,零件的外径为16cm,要求它的壁厚x,需要先求出内径AB,现用一个交叉钳(AD与BC相等)去量,若测得OA︰OD=OB︰OC=3︰1,CD=5cm,你能求零件的壁厚x吗?