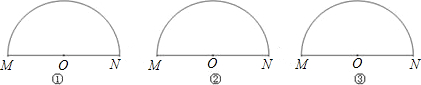
四边形ABCD是正方形.
(1)如图1,点G是BC边上任意一点(不与B、C两点重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E.求证:△ABF≌△DAE;
(2)在(1)中,线段EF与AF、BF的等量关系是 (直接写出结论即可,不需要证明);
(3)如图2,点G是CD边上任意一点(不与C、D两点重合),连接AG,作BF⊥AG于点F,DE⊥AG于点E.那么图中全等三角形是 ,线段EF与AF、BF的等量关系是 (直接写出结论即可,不需要证明).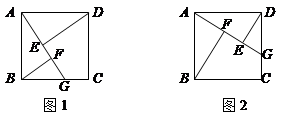
先化简,再求值: ,其中
,其中
已知:如图,直线AB与直线BC相交于点B,点D是直线BC上一点,求作:点E,使直线DE∥AB,且点E到B、D两点的距离相等.(尺规作图,要求在题目的原图中完成作图)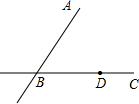
若关于x的不等式组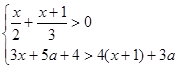 恰有三个整数解,求实数a的取值范围。
恰有三个整数解,求实数a的取值范围。
在直角坐标系xOy中,已知点P是反比例函数y= (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的 ?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
?若存在,试求出所有满足条件的M点的坐标;若不存在,试说明理由.
(1)在图①的半径为R的半圆O内(含弧),求出一边落在直径MN上的最大的正三角形的面积?
(2)在图②的半径为R的半圆O内(含弧),求出一边落在直径MN上的最大的正方形的面积?
问题解决
(3)如图③,现有一块半径R=6的半圆形钢板,是否可以裁出一边落在MN上的面积最大的矩形?若存在,请说明理由,并求出这个矩形的面积;若不存在,说明理由?