某企业的某种产品产量与单位成本统计数据如下:
| 月份 |
1 |
2 |
3 |
4 |
5 |
6 |
| 产量(千件) |
2 |
3 |
4 |
3 |
4 |
5 |
| 单位成本(元/件) |
73 |
72 |
71 |
73 |
69 |
68 |

(用最小二乘法求线性回归方程系数公式
注: ,
, )
)
(1)试确定回归方程;
(2)指出产量每增加1 件时,单位成本下降多少?
(3)假定产量为6 件时,单位成本是多少?单位成本为70元/件时,产量应为多少件?
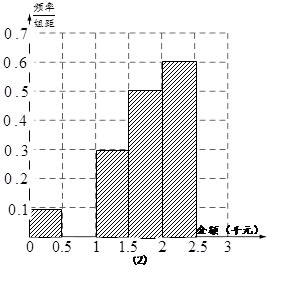
某网络营销部门为了统计某市网友2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天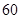 名网友的网购金额情况,得到如下数据统计表(如图):
名网友的网购金额情况,得到如下数据统计表(如图):
若网购金额超过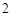 千元的顾客定义为“网购达人”,网购金额不超过
千元的顾客定义为“网购达人”,网购金额不超过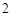 千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为
千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为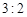 .
.
(1)试确定 ,
,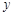 ,
,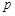 ,
,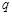 的值,并补全频率分布直方图(如图(2)).
的值,并补全频率分布直方图(如图(2)).
(2)该营销部门为了进一步了解这 名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定
名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定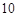 人,若需从这
人,若需从这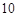 人中随机选取
人中随机选取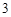 人进行问卷调查.设
人进行问卷调查.设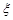 为选取的
为选取的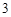 人中“网购达人”的人数,求
人中“网购达人”的人数,求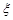 的分布列和数学期望.
的分布列和数学期望.
已知函数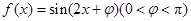 的图像经过点
的图像经过点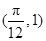 .
.
(1)求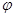 的值;
的值;
(2)在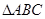 中,
中,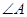 、
、 、
、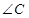 所对的边分别为
所对的边分别为 、
、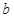 、
、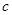 ,若
,若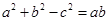 ,且
,且 .求
.求 .
.
一次函数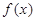 是
是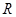 上的增函数,
上的增函数,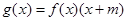 ,已知
,已知 .
.
(1)求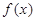 ;
;
(2)若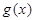 在
在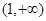 单调递增,求实数
单调递增,求实数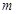 的取值范围;
的取值范围;
(3)当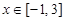 时,
时,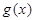 有最大值
有最大值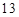 ,求实数
,求实数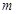 的值.
的值.
已知平面内两点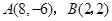 .
.
(1)求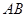 的中垂线方程;
的中垂线方程;
(2)求过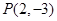 点且与直线
点且与直线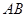 平行的直线
平行的直线 的方程;
的方程;
(3)一束光线从 点射向(2)中的直线
点射向(2)中的直线 ,若反射光线过点
,若反射光线过点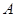 ,求反射光线所在的直线方程.
,求反射光线所在的直线方程.
已知直三棱柱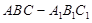 中,
中,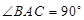 ,
,
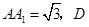 是
是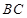 中点,
中点,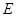 是
是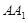 中点.
中点.
(1)求三棱柱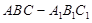 的体积;
的体积;
(2)求证: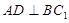 ;
;
(3)求证: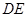 ∥面
∥面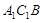 .
.