(本题8分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,
PA=AB=2,M, N分别为PA, BC的中点.
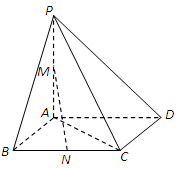
(Ⅰ)证明:MN∥平面PCD;
(Ⅱ)求MN与平面PAC所成角的正切值.
(本小题满分12分)
已知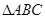 的内角为A、B、C的对边分别为
的内角为A、B、C的对边分别为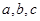 ,B为锐角,向量
,B为锐角,向量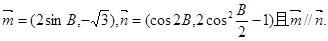
(1)求B的大小;
(2)如果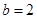 ,求
,求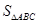 的最大值.
的最大值.
(本小题满分12分)
已知函数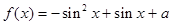 ,若
,若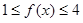 对一切
对一切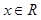 恒成立.求实数
恒成立.求实数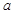 的取值范围.(16分)
的取值范围.(16分)
(本小题满分12分)
已知甲、乙两个工厂在今年的1月份的利润都是6万,且乙厂在2月份的利润是8万元.若甲、乙两个工厂的利润(万元)与月份x之间的函数关系式分别符合下列函数模型:f(x)=a1x2—4x+6,g(x)=a2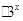 +b2(a1,a2,b2∈R).
+b2(a1,a2,b2∈R).
(1)求函数f(x)与g(x)的解析式;
(2)求甲、乙两个工厂今年5月份的利润;
(3)在同一直角坐标系下画出函数f(x)与g(x)的草图,并根据草图比较今年1—10月份甲、乙两个工厂的利润的大小情况.
(本小题满分12分)
设
 ,若方程
,若方程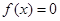 有两个均小于2的不同的实数根,则此时关于
有两个均小于2的不同的实数根,则此时关于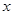 的不等式
的不等式 是否对一切实数
是否对一切实数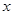 都成立?并说明理由。
都成立?并说明理由。
(本小题满分12分)
已知函数 的最小正周期为
的最小正周期为 ,最小值为
,最小值为 ,图象过点
,图象过点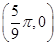 ,(1)求
,(1)求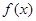 的解析式;(2)求满足
的解析式;(2)求满足 且
且
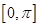 的
的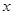 的集合.
的集合.