(本题10分)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,M为线段AB的中点,将△ACD沿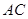 折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
折起,使平面ACD⊥平面ABC,得到几何体D-ABC,如图2所示.
(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求二面角A-CD-M的余弦值.
(12分
|
)已知函数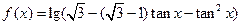 . (1)求函数
. (1)求函数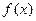 的定义域. (2)若
的定义域. (2)若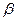 是两个模长为2的向量
是两个模长为2的向量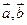 的夹角,且不等式
的夹角,且不等式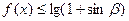 对于定义域内
对于定义域内
 恒成立,求
恒成立,求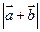 的取值范围.
的取值范围.
(12分)已知数列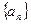 满足
满足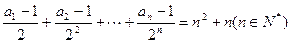 .
.
(1)求数列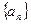 的通项公式. (2)求数列
的通项公式. (2)求数列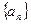 前
前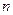 项和
项和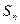 .
.
(12)如图,四棱锥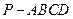 的底面
的底面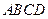 为正方形,
为正方形,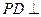 平面
平面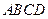 ,
,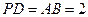 ,
,
 ,
,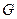 分别为
分别为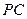 ,
,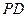 和
和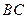 的中点. (1)求证
的中点. (1)求证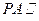 平面
平面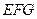 .(2)求异面直线
.(2)求异面直线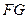 与
与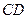 所成角的正切值.
所成角的正切值.
(12分)已知函数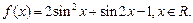
(1)求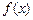 的最小正周期及
的最小正周期及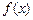 取得最大值时x的集合.
取得最大值时x的集合.
(2)在平面直角坐标系中画出函数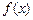 在
在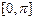 上的图象(在图上标明关键点的坐标)
上的图象(在图上标明关键点的坐标)
设函数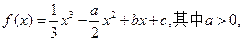 曲线
曲线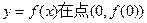 处的切线方程为y=1。
处的切线方程为y=1。
(1)确定b,c的值。
(2)若过点(0,2)能且只能作曲线y=f(x)的一条切线,求a的取值范围。