题满分12分）设函数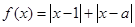
（1）若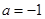
，解不等式
；
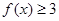（2）如果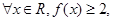
求a的取值范围.
已知函数
，若
在x=1处的切线方程是3x+y-6=0
（Ⅰ）求函数的解析式；
（Ⅱ）若对任意的
，都有
成立，求函数
的最值.
已知椭圆C的中心在原点，焦点在x轴上，它的一个顶点恰好是抛物线
的焦点，离心率等于
.
（Ⅰ）求椭圆C的方程；
（Ⅱ）过椭圆C的右焦点F作直线
交椭圆C于A，B两点，交y轴于M点，若
,求证
为定值.
设数列
的前n项和为
，
为等比数列，且
.
（1）求数列和的通项公式；
（2）设
，求数列
的前n项和
。
已知在四棱锥P-ABCD中，AD//BC, 
PA=PD=AD=2BC=2CD,E,F分别为AD,PC的中点. 
（Ⅰ）求证
平面PBE;
（Ⅱ）求证PA//平面BEF;
（Ⅲ）若PB=AD,求二面角F-BE-C的大小.
在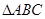
中，内角A,B,C的对边分别为a,b,c，已知B="C," 2b=
.
（Ⅰ）求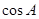
得值.
（Ⅱ）求
的值.