在四棱锥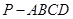 中,
中, 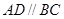 ,
,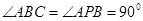 ,点
,点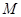 是线段
是线段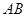 上的一点,且
上的一点,且 ,
,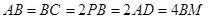 .
.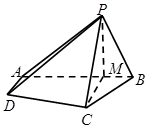
(1)证明:面 面
面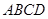 ;
;
(2)求直线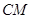 与平面
与平面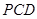 所成角的正弦值.
所成角的正弦值.
如图,海上有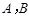 两个小岛相距10
两个小岛相距10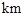 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为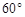 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至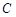 处进行作业,且
处进行作业,且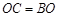 .设
.设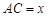
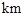 。
。
(1)若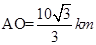 ,求出
,求出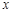 的取值;
的取值;
(2)用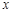 分别表示
分别表示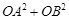 和
和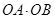 ,并求出
,并求出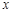 的取值范围.
的取值范围.
集合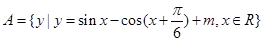 ,
,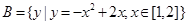 ,若命题
,若命题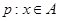 ,命题
,命题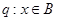 ,且
,且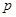 是
是 必要不充分条件,求实数
必要不充分条件,求实数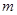 的取值范围。
的取值范围。
设函数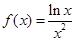 ,
,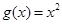 .
.
(1)求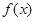 的极大值;
的极大值;
(2)求证:
(3)当方程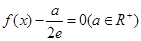 有唯一解时,试探究函数
有唯一解时,试探究函数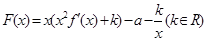 与
与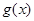 的图象在其公共点处是否存在公切线,若存在.研究
的图象在其公共点处是否存在公切线,若存在.研究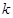 的值的个数;若不存在,请说明理由.
的值的个数;若不存在,请说明理由.
已知数列 中,
中, 且点
且点 在直线
在直线 上。
上。
(1)求数列 的通项公式;
的通项公式;
(2)若函数 求函数
求函数 的最小值;
的最小值;
(3)设 表示数列
表示数列 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于 的整式
的整式 ,使得
,使得 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立?若存在,写出
恒成立?若存在,写出 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。