(本题10分)已知函数
(1)利用函数单调性的定义,判断函数 在
在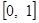 上的单调性;
上的单调性;
(2)若 ,求函数
,求函数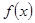 在
在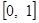 上的最大值
上的最大值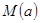 。
。
(本小题满分12分)已知正项等比数列 中,
中, ,且
,且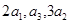 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)设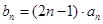 ,求数列
,求数列 的前n项和
的前n项和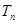 .
.
(本小题满分12分)已知函数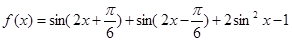 .
.
(1)求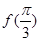 的值;
的值;
(2)求函数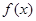 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(3)说明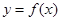 的图像是如何由函数
的图像是如何由函数 的图像变换所得.
的图像变换所得.
【改编】(本小题满分12分)贵广高速铁路自贵阳北站起,经黔南州、黔东南、广西桂林、贺州、广东肇庆、佛山终至广州南站.其中广东省内有怀集站、广宁站、肇庆东站、三水南站、佛山西站、广州南站共6个站.记者对广东省内的6个车站随机抽取3个进行车站服务满意度调查.
(1)求抽取的车站中不含佛山市内车站(包括三水南站和佛山西站)的概率;
(2)设抽取的车站中含有肇庆市内车站(包括怀集站、广宁站、肇庆东站)个数为X,求X的分布列及其均值(即数学期望).
对于函数 ,若
,若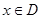 时,恒有
时,恒有 成立,则称函数
成立,则称函数 是
是 上 的“
上 的“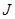 函数”.
函数”.
(Ⅰ)当函数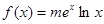 是定义域上的“
是定义域上的“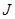 函数”时,求实数
函数”时,求实数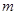 的取值范围;
的取值范围;
(Ⅱ)若函数 为
为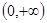 上的“
上的“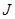 函数”.
函数”.
(ⅰ)试比较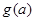 与
与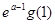 的大小(其中
的大小(其中 );
);
(ⅱ)求证:对于任意大于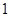 的实数
的实数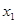 ,
, ,
,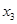 ,,
,,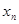 均有
均有 .
.
(本小题满分13分)已知椭圆 的离心率为
的离心率为 ,且过点
,且过点 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,设 ,满足
,满足 .
.
(ⅰ)试证 的值为定值,并求出此定值;
的值为定值,并求出此定值;
(ⅱ)试求四边形ABCD面积的最大值.