已知f(x)=x3+x(x∈R),
(1)判断f(x)在(-∞,+∞)上的单调性,并证明;
(2)求证:满足f(x)=a(a为常数)的实数x至多只有一个.
设曲线C的方程是y=x3-x,将C沿x轴、y轴正向分别平移t、s单位长度后,得到曲线C1.
(1)写出曲线C1的方程;
(2)证明:曲线C与C1关于点A(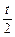 ,
,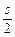 )对称.
)对称.
已知点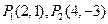 ,求出下列情况,点
,求出下列情况,点 分有向线段
分有向线段 所成的比
所成的比 及点
及点 的坐标:
的坐标:
⑴点 在
在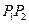 上,且
上,且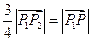 ;
;
⑵点 在
在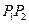 的延长线上,
的延长线上, ;
;
⑶点 在
在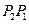 的延长线上,
的延长线上,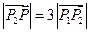 .
.
已知点A(-1,6)和B(3,0),在直线AB上求一点P,使|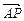 |=
|=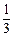 |
| |.
|.
已知函数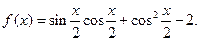
(1)将函数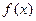 化简成
化简成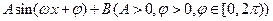 的形式,并指出
的形式,并指出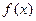 的周期;
的周期;
(2)求函数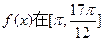 上的最大值和最小值.
上的最大值和最小值.
已知数列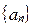 满足
满足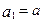 ,
, 我们知道当a取不同的值时,得到不同的数列,如当
我们知道当a取不同的值时,得到不同的数列,如当 时,得到无穷数列:
时,得到无穷数列: 当
当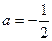 时,得到有穷数列:
时,得到有穷数列: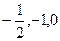 .
.
(Ⅰ)求当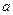 为何值时
为何值时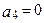 ;
;
(Ⅱ)设数列 满足
满足 ,
, 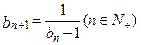 ,求证:
,求证: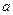 取数列
取数列 中的任一个数,都可以得到一个有穷数列
中的任一个数,都可以得到一个有穷数列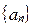 ;
;
(Ⅲ)若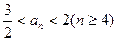 ,求
,求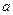 的取值范围.
的取值范围.