某家电商场计划用32400元购进“家电下乡”指定产品中的电视机、冰箱、洗衣机共15台．三种家电的进价和售价如下表所示：
 价格种类 |
进价（元/台） |
售价（元/台） |
| 电视机 |
2000 |
2100 |
| 冰箱 |
2400 |
2500 |
| 洗衣机 |
1600 |
1700 |
（1）在不超出现有资金的前提下，若购进电视机的数量和冰箱的数量相同，洗衣机数量不大于电视机数量的一半，商场有哪几种进货方案？
（2）国家规定：农民购买家电后，可根据商场售价的13%领取补贴．在（1）的条件下，如果这15台家电全部销售给农民，国家财政最多需补贴农民多少元？
已知抛物线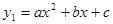
的顶点坐标为（
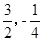）且经过点A（1，0），直线
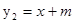恰好也经过点A
（1）分别求抛物线和直线的解析式
（2）当x取何值时，函数值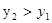
（3）当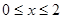
时，直接写出
的最小值分别为多少？
在一个不透明的盒子里，装有四个分别标有数字1,2,3,4的小球，它们的形状、大小、质地等完全相同。小米先从盒子中随机取出一个小球，记下数字为x，且不放回盒子，再由小华随机取出一个小球，记下数字为y．
（1）用列表法或画树状图表示出（x, y）的所有可能出现的结果；
（2）求小米、小华各取一次小球所确定的点（x, y）落在反比例函数
的图象上的概率；
判断下列二次函数的图象与x轴有无交点，若有请求出交点坐标；若无请说明理由．
（1）
（2）
如图是抛物线
的一部分，且其过点（3,0），对称轴为直线x=1，则下列结论正确的有_________
①abc＞0
②方程
有两个不相等的实数根
③a-b+c=0
④当x＞0时，y随x的增大而增大
⑤不等式
的解为x＞3
⑥3a+2c＜0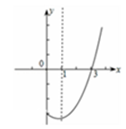
探索证明如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD，BD， BC，AC的中点．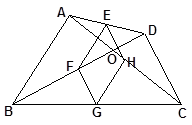
（1）求证：四边形EFGH是平行四边形；
（2）当四边形ABCD满足一个什么条件时，四边形EFGH是菱形？并证明你的结论．
（3）当AB和CD满足什么条件时，四边形EFGH是正方形．（直接写出结论，不必写证明过程）