求函数 的定义域
的定义域
在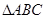 中,
中,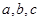 分别为内角
分别为内角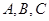 的对边,且
的对边,且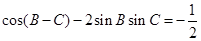 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若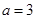 ,
,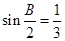 ,求边
,求边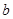 的长.
的长.
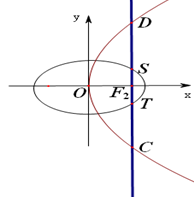
如图,椭圆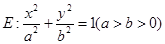 的右焦点
的右焦点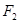 与抛物线
与抛物线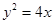 的焦点重合,过
的焦点重合,过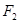 作与
作与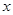 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于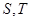 ,而与抛物线交于
,而与抛物线交于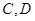 两点,且
两点,且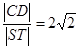 .
.
(Ⅰ)求椭圆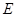 的方程;
的方程;
(Ⅱ)若过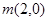 的直线与椭圆
的直线与椭圆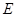 相交于两点
相交于两点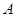 和
和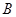 ,
,
设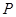 为椭圆
为椭圆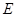 上一点,且满足
上一点,且满足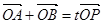 (
(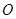 为坐标原点),求实数
为坐标原点),求实数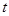 的取值范围.
的取值范围.
已知函数 ,且
,且 。
。
(1)若函数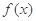 在
在 处的切线与
处的切线与 轴垂直,求
轴垂直,求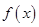 的极值。
的极值。
(2)若函数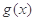 在
在 ,求实数a的值。
,求实数a的值。
如图所示,已知AC ⊥平面CDE, BD ∥AC ,  为等边三角形,F为ED边上的中点,且
为等边三角形,F为ED边上的中点,且 ,
,
(Ⅰ)求证:CF∥面ABE;
(Ⅱ)求证:面ABE ⊥平面BDE;
(Ⅲ)求该几何体ABECD的体积。
某校从参加市联考的甲、乙两班数学成绩110分以上的同学中各随机抽取8人,将这16人的数学成绩编成如下茎叶图.
(Ⅰ)茎叶图中有一个数据污损不清(用△表示),若甲班抽出来的同学平均成绩为122分,试推算这个污损的数据是多少?
(Ⅱ)现要从成绩在130分以上的5位同学中选2位作数学学习方法介绍,请将所有可能的结果列举出来,并求选出的两位同学不在同一个班的概率.