在△ABC中,角A,B,C所对的边长分别是a,b,c.
(1)若sin C + sin(B-A)=" sin" 2A,试判断△ABC的形状;
(2)若△ABC的面积S = 3 ,且c =
,且c =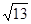 ,C =
,C = ,求a,b的值.
,求a,b的值.
(本小题满分8分)设 的内角
的内角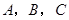 所对边的长分别为
所对边的长分别为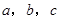 ,向量
,向量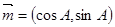 ,
, ,若
,若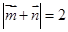
(1)求角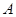 的大小;
的大小;
(2)若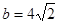 ,
,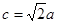 ,求
,求 的面积.
的面积.
(本小题满分8分)设等比数列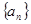 的前
的前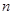 项和为
项和为 ,若
,若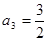 ,
,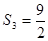 ,求数列
,求数列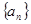 的通项公式.
的通项公式.
(本小题满分12分)已知函数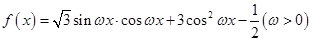 , 且
, 且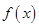 的最小正周期为
的最小正周期为 .
.
(1)求函数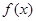 的解析式及函数
的解析式及函数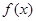 的对称中心;
的对称中心;
(2)若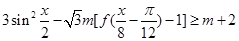 对任意
对任意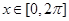 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
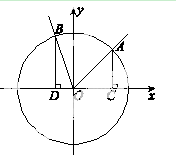
(本小题满分10分)如图,在直角坐标系 中,角
中,角 的顶点是原点,始边与
的顶点是原点,始边与 轴正半轴重合,终边交单位圆于点
轴正半轴重合,终边交单位圆于点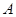 ,且
,且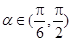 .将角
.将角 的终边按逆时针方向旋转
的终边按逆时针方向旋转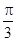 ,交单位圆于点
,交单位圆于点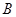 .记
.记 .
.
(1)若 ,求
,求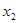 ;
;
(2)分别过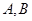 作
作 轴的垂线,垂足依次为
轴的垂线,垂足依次为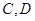 .记△
.记△ 的面积为
的面积为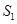 ,△
,△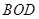 的面积为
的面积为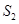 .若
.若 ,求角
,求角 的值.
的值.
已知函数 .
.
(1)求函数 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)当 时,求
时,求 的最大值,并求此时对应的
的最大值,并求此时对应的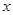 的值.
的值.