如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点, HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.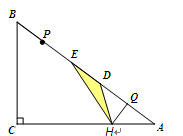
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式并求y的最大值;
(3)当x为何值时,△HDE为等腰三角形?
计算: .
如图,已知锐角三角形 内接于圆 , 于点 ,连接 .
(1)若 ,
①求证: .
②当 时,求 面积的最大值.
(2)点 在线段 上, ,连接 ,设 , , 是正数),若 ,求证: .

设二次函数 , 是实数).
(1)甲求得当 时, ;当 时, ;乙求得当 时, .若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由.
(2)写出二次函数图象的对称轴,并求该函数的最小值(用含 , 的代数式表示).
(3)已知二次函数的图象经过 和 两点 , 是实数),当 时,求证: .
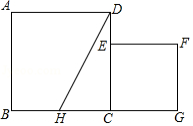
如图,已知正方形 的边长为1,正方形 的面积为 ,点 在 边上,点 在 的延长线上,设以线段 和 为邻边的矩形的面积为 ,且 .
(1)求线段 的长;
(2)若点 为 边的中点,连接 ,求证: .
方方驾驶小汽车匀速地从 地行驶到 地,行驶里程为480千米,设小汽车的行驶时间为 (单位:小时),行驶速度为 (单位:千米 小时),且全程速度限定为不超过120千米 小时.
(1)求 关于 的函数表达式;
(2)方方上午8点驾驶小汽车从 地出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达 地,求小汽车行驶速度 的范围.
②方方能否在当天11点30分前到达 地?说明理由.