(本小题满分16分)
已知等差数列 中,
中, ,令
,令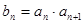 ,数列
,数列 的前
的前 项和为
项和为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求证: ;
;
(3)是否存在正整数 ,且
,且 ,使得
,使得 ,
, ,
, 成等比数列?若存在,求出
成等比数列?若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(文)已知7件产品中有4件正品和3件次品.
(1)从这7件产品中一次性随机抽出3件,求抽出的产品中恰有1件正品数的概率;
(2)从这7件产品中一次性随机抽出4件,求抽出的产品中正品件数不少于次品件数的概率.
(本小题满分16分)定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意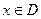 ,存在常数
,存在常数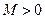 ,都有
,都有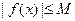 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中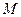 称为函数
称为函数 的上界.
的上界.
已知函数 ;
; .
.
(1)当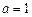 时,求函数
时,求函数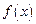 在
在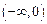 上的值域,并判断函数
上的值域,并判断函数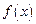 在
在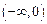 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数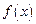 在
在 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 的取值范围;
的取值范围;
(3)若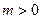 ,函数
,函数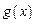 在
在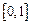 上的上界是
上的上界是 ,求
,求 的取值范围.
的取值范围.
(本小题满分16分)设数列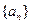 的前n项和为
的前n项和为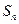 ,数列
,数列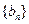 满足:
满足:  ,且数列
,且数列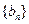 的前
的前
n项和为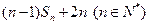 .
.
(1) 求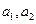 的值;
的值;
(2) 求证:数列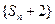 是等比数列;
是等比数列;
(3) 抽去数列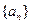 中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列
中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列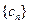 ,若
,若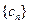 的前n项和为
的前n项和为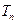 ,求证:
,求证: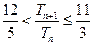 .
.
(本小题满分15分)已知椭圆 的左焦点为F,左右顶点分别为A、C,
的左焦点为F,左右顶点分别为A、C,
上顶点为B,过F,B,C三点作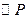 ,其中圆心P的坐标为
,其中圆心P的坐标为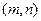 .
.
(1) 若椭圆的离心率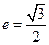 ,求
,求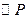 的方程;
的方程;
(2)若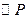 的圆心在直线
的圆心在直线 上,求椭圆的方程.
上,求椭圆的方程.
(本小题满分15分)已知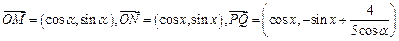
(1)当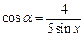 时,求函数
时,求函数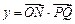 的最小正周期;
的最小正周期;
(2)当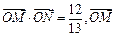 ∥
∥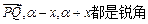 时,求
时,求 的值.
的值.