如图1,在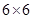 的方格纸中,给出如下三种变换:
的方格纸中,给出如下三种变换: 变换,
变换, 变换,
变换,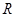 变换.
变换.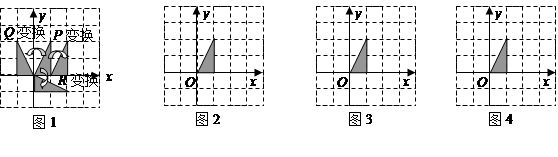
将图形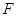 沿
沿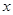 轴向右平移1格得图形
轴向右平移1格得图形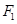 ,称为作
,称为作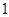 次
次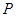 变换;
变换;
将图形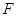 沿
沿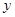 轴翻折得图形
轴翻折得图形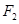 ,称为作1次
,称为作1次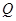 变换;
变换;
将图形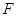 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转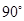 得图形
得图形 ,称为作1次
,称为作1次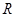 变换.
变换.
规定: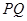 变换表示先作1次
变换表示先作1次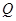 变换,再作1次
变换,再作1次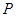 变换;
变换;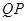 变换表示先作
变换表示先作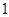 次
次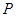 变换,再依1次
变换,再依1次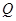 变换;
变换;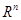 变换表示作
变换表示作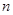 次
次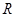 变换.
变换.
解答下列问题:
(1)作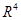 变换相当于至少作 次
变换相当于至少作 次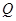 变换;
变换;
(2)请在图2中画出图形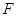 作
作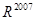 变换后得到的图形
变换后得到的图形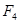 ;
;
(3)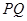 变换与
变换与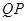 变换是否是相同的变换?请在图3中画出
变换是否是相同的变换?请在图3中画出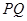 变换后得到的图形
变换后得到的图形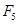 ,在图4中画出
,在图4中画出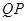 变换后得到的图形
变换后得到的图形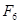 .
.
如图,海上有一灯塔P,在它周围6海里内有暗礁.一艘海轮以18海里/时的速度由西向东方向航行,行至A点处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,如果海轮不改变方向继续前进有没有触礁的危险?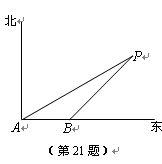
解分式方程: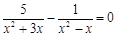 .
.
(1)计算: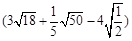 ÷
÷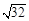 ;
;
(2)分解因式: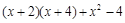
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
信息读取:
(1)甲、乙两地之间的距离为km;
(2)请解释图中点B的实际意义;
图象理解:
(3)求慢车和快车的速度;
(4)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
问题解决:
(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
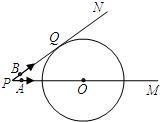
如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A,B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动.设运动时间为ts.
(1)求PQ的长;
(2)当t为何值时,直线AB与⊙O相切?