已知函数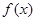 =
=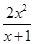 ,
, .
.
(1)求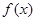 在x∈[0,1]上的值域;
在x∈[0,1]上的值域;
(2)若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,则求 的取值范围.
的取值范围.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=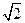 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.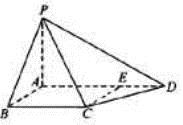
给定抛物线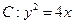 ,
,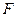 是抛物线
是抛物线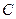 的焦点,过点
的焦点,过点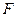 的直线
的直线 与
与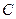 相交于
相交于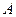 、
、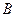 两点,
两点, 为坐标原点.
为坐标原点.
(1)设 的斜率为1,求以
的斜率为1,求以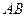 为直径的圆的方程;
为直径的圆的方程;
(2)设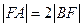 ,求直线
,求直线 的方程.
的方程.
已知 .
.
(1)若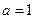 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若 求函数
求函数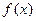 的单调区间;
的单调区间;
(3)若不等式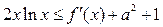 恒成立,求实数
恒成立,求实数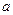 的取值范围.
的取值范围.
如图,AB是⊙O的一条切线,切点为B,ADE、CFD都是⊙O的割线,AC=AB.
(1)证明:AC2=AD·AE
(2)证明:FG∥AC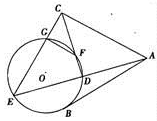
在 中,内角
中,内角 所对边长分别为
所对边长分别为 ,
,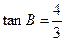 ,
,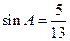 .
.
(1)求 ;
;
(2)若 的面积是1,求
的面积是1,求 .
.