甲、乙两车同时从 地出发,以各自的速度匀速向
地出发,以各自的速度匀速向 地行驶.甲车先到达
地行驶.甲车先到达 地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离
地,停留1小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为每小时60千米.下图是两车之间的距离 (千米)与乙车行驶时间
(千米)与乙车行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象.
(1)请将图中的( )内填上正确的值,并直接写出甲车从 到
到 的行驶速度;
的行驶速度;
(2)求从甲车返回到与乙车相遇过程中 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围.
的取值范围.
(3)求出甲车返回时行驶速度及 、
、 两地的距离.
两地的距离.
现有若干张相同的半圆形纸片,点O是圆心,直径AB的长是12cm,C是半圆弧上的一点(点C与点A、B不重合),连接AC、BC.
(1)沿AC、BC剪下△ABC,则△ABC是 三角形(填“锐角”、“直角”或“钝角”);
(2)分别取半圆弧上的点E、F和直径AB上的点G、H.已知剪下的由这四个点顺次连接构成的四边形是一个边长为6cm的菱形.请用直尺和圆规在图中作出一个符合条件的菱形(保留作图痕迹,不要求写作法);
(3)经过数次探索,小明猜想,对于半圆弧上的任意一点C,一定存在线段AC上的点M、线段BC上的点N和直径AB上的点P、Q,使得由这四个点顺次连接构成的四边形是一个边长为4cm的菱形.小明的猜想是否正确?请说明理由.

已知二次函数 的自变量x的部分取值和对应函数值y如下表:
|
x |
… |
﹣1 |
0 |
1 |
2 |
3 |
… |
|
y |
… |
4 |
3 |
0 |
﹣5 |
﹣12 |
… |
(1)求二次函数 的表达式;
(2)将二次函数 的图象向右平移k(k>0)个单位,得到二次函数 的图象,使得当﹣1<x<3时,y随x增大而增大;当4<x<5时,y随x增大而减小.请写出一个符合条件的二次函数 的表达式y= ,实数k的取值范围是 ;
(3)A、B、C是二次函数 的图象上互不重合的三点.已知点A、B的横坐标分别是m、m+1,点C与点A关于该函数图象的对称轴对称,求∠ACB的度数.
在四边形ABCD中,O是边BC上的一点.若 ,则点O叫做该四边形的“等形点”.
(1)正方形 “等形点”(填“存在”或“不存在”);
(2)如图,在四边形ABCD中,边BC上的点O是四边形ABCD的“等形点”.已知 , , ,连接AC,求AC的长;
(3)在四边形EFGH中,EH∥FG.若边FG上的点O是四边形EFGH的“等形点”,求 的值.

第十四届国际数学教育大会(ICME﹣14)会徽的主题图案有着丰富的数学元素,展现了我国古代数学的文化魅力,其右下方的“卦”是用我国古代的计数符号写出的八进制数3745.八进制是以8作为进位基数的数字系统,有0~7共8个基本数字.八进制数3745换算成十进制数是3×83+7×82+4×81+5×80=2021,表示ICME﹣14的举办年份.
(1)八进制数3746换算成十进制数是 ;
(2)小华设计了一个n进制数143,换算成十进制数是120,求n的值.

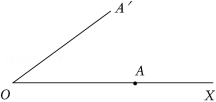
如图,点A在射线OX上,OA=a.如果OA绕点O按逆时针方向旋转n°(0<n≤360)到OA′,那么点A′的位置可以用(a,n°)表示.
(1)按上述表示方法,若a=3,n=37,则点A′的位置可以表示为 ;
(2)在(1)的条件下,已知点B的位置用(3,74°)表示,连接A′A、A′B.求证:A′A=A′B.