已知动点 到点
到点 的距离,等于它到直线
的距离,等于它到直线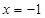 的距离.
的距离.
(Ⅰ)求点 的轨迹
的轨迹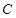 的方程;
的方程;
(Ⅱ)过点 任意作互相垂直的两条直线
任意作互相垂直的两条直线 ,分别交曲线
,分别交曲线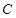 于点
于点 和
和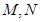 .设线段
.设线段 ,
,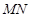 的中点分别为
的中点分别为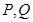 ,求证:直线
,求证:直线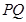 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求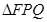 面积的最小值.
面积的最小值.
某校伙食长期以面粉和大米为主食,面食每100 g含蛋白质6个单位,含淀粉4个单位,售价0.5元,米食每100 g含蛋白质3个单位,含淀粉7个单位,售价0.4元,学校要求给学生配制盒饭,每盒盒饭至少有8个单位的蛋白质和10个单位的淀粉,问应如何配制盒饭,才既科学又费用最少?
设计一幅宣传画,要求画面面积为4840 cm2,画面的宽与高的比为λ(λ<1),画面的上下各留8 cm的空白,左右各留5 cm的空白,问怎样确定画面的高与宽的尺寸,能使宣传画所用纸张面积最小?如果λ∈,那么λ为何值时,能使宣传画所用纸张面积最小
围建一个面积为360 m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2 m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用为y(单位:元).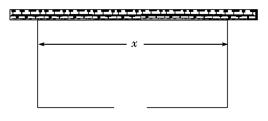
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
设a、b、c均为实数,求证:++≥++
已知a、b、c∈R,求证:a2+b2+c2+4≥ab+3b+2c.