(1)过点P(0,0),Q(4,2),R(-1,-3)三点的圆的标准方程式什么?
(2)已知动点M到点A(2,0)的距离是它到点B(-1,0)的距离的 倍,求:(1)动点M的轨迹方程;(2)根据
倍,求:(1)动点M的轨迹方程;(2)根据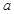 取值范围指出轨迹表示的图形.
取值范围指出轨迹表示的图形.
.如图,四边形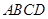 为矩形,
为矩形,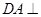 平面
平面 ,
, ,
, 平面
平面 于点
于点 ,且点
,且点 在
在 上.
上.
(1)求证: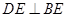 ;(2)求四棱锥
;(2)求四棱锥 的体积;
的体积;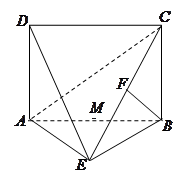
(3)设点 在线段
在线段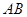 上,且
上,且 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得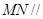 平面
平面 .
.
数列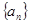 的前n项和为
的前n项和为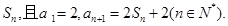
(1)求数列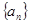 的通项公式;
的通项公式;
(2)等差数列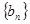 的各项为正,其前n项和为
的各项为正,其前n项和为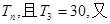
 成等比数列,求
成等比数列,求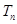 的最小值.
的最小值.
在 中,已知
中,已知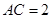 ,
, ,
,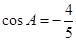 .
.
(1)求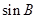 的值;(2)求
的值;(2)求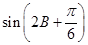 的值.
的值.
.围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建围墙的总费用为y (单位:元).
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
如图,在三棱锥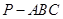 中,
中,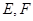 分别为
分别为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)若平面 平面
平面 ,且
,且 ,
,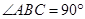 ,
,
求证:平面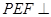 平面
平面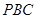 .
.