(1)求 的定义域;(2)设
的定义域;(2)设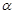 是第二象限的角,且tan
是第二象限的角,且tan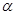 =
=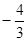 ,求
,求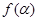 的值.
的值.
(本小题满分12分)
如图所示,圆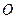

 的直径
的直径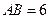 ,
,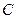 为圆周上一点,
为圆周上一点, ,过
,过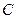 作圆的切线
作圆的切线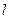 ,过
,过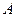 作
作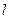 的垂线
的垂线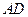 ,垂足为
,垂足为 ,求∠DAC
,求∠DAC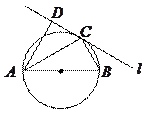
(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是边长为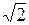 的正方形,E为P
的正方形,E为P C的中点,PB=PD.
C的中点,PB=PD.
(1)证明:BD ⊥平面PAC.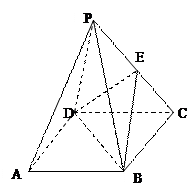
(2)若PA=PC=2,求三棱锥E-BCD的体积。
已知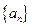 是首项为19,公差为-4的等差数列,
是首项为19,公差为-4的等差数列,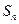 为
为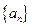 的前
的前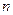 项和.
项和.
(Ⅰ)求通项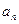 及
及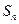 ;
;
(Ⅱ)设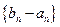 是首项为1,公比为2的等比数列,求数列
是首项为1,公比为2的等比数列,求数列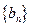 的通项公式及其前
的通项公式及其前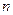 项和
项和 .
.
(本小题满分10分)设锐角三角形ABC的内角A,B,C的对边长分别为 ,b ,c ,
,b ,c ,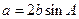 .
.
(1)求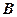 的大小;
的大小;
(2)若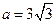 ,
, ,求b.
,求b.
(本小题满分10分)选修4-5:不等式选讲
(Ⅰ)求证:已知 都是正实数,求证:
都是正实数,求证: ;
;
(Ⅱ)求证:已知 都是正数,求证:
都是正数,求证: .
.