在四边形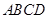 中,
中, ,且
,且 .取
.取 的中点
的中点 ,连结
,连结 .
.
(1)试判断三角形 的形状;
的形状;
(2)在线段 上,是否存在点
上,是否存在点 ,使
,使 .若存在,请求出
.若存在,请求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上,向内放入两个半径为5cm的钢球,测得上面一个钢球顶部高DC=16cm(钢管的轴截面如图所示),求钢管的内直径AD的长.
若两圆的圆心距d满足等式 ,且两圆的半径是方程
,且两圆的半径是方程 的两个根,试判断这两圆的位置关系.
的两个根,试判断这两圆的位置关系.
已知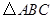 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示.
(1)分别写出图中点 的坐标;
的坐标;
(2)画出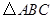 绕点
绕点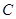 按顺时针方向旋转
按顺时针方向旋转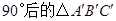 ;
;
(3)求点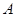 旋转到点
旋转到点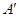 所经过的路线长(结果保留
所经过的路线长(结果保留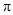 ).
).
在等腰直角△ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转180°,点B落在点B′处,作出点B′并求BB′的长度.
如图是某汽车的标志,它可以看作是由什么“基本图案”通过怎样旋转得到的?每次旋转了多少度?