对给定的一张矩形纸片 进行如下操作:先沿 折叠,使点 落在 边上(如图① ,再沿 折叠,这时发现点 恰好与点 重合(如图②
(1)根据以上操作和发现,求 的值;
(2)将该矩形纸片展开.
①如图③,折叠该矩形纸片,使点 与点 重合,折痕与 相交于点 ,再将该矩形纸片展开.求证: ;
②不借助工具,利用图④探索一种新的折叠方法,找出与图③中位置相同的 点,要求只有一条折痕,且点 在折痕上,请简要说明折叠方法.(不需说明理由)

(年贵州黔东南12分)黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠,若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.
(年黑龙江龙东地区10分)如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).
(1)求点D的坐标.
(2)求直线BC的解析式.
(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
(年贵州黔东南12分)黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠,若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.
(年河北省13分)某景区的环形路是边长为800米的正方形ABCD,如图,现有1号,2号两游览车分别从出口A和经典C同时出发,1号车顺时针,2号车逆时针沿环形路连续循环行驶,供游客随时乘车(上,下车的时间忽略不计),两车的速度均为200米/分.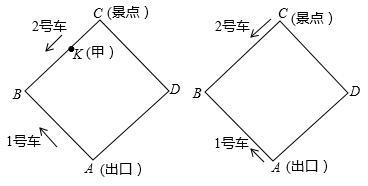
探究:设行驶时间为t分
(1)当0≤t≤s时,分别写出1号车,2号车在左半环线离出口A的路程y1,y2(米)与t的函数关系式,并求出当两车相距的路程是400米时t的值;
(2)t为何值时,1号车第三次恰好经过点C?,并直接写出这一段时间内它与2号车相遇过的次数.
发现:如图,游客甲在BC上一点K(不与点B,C重合)处候车,准备乘车到出口A,设CK=x米.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车;
比较哪种情况用时较多?(含候车时间)
决策:已知游客乙在DA上从D向出口A走去,步行的速度是50米/分,当行进到DA上一点P(不与D,A重合)时,刚好与2号车相遇.
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由;
(2)设PA=s(0<s<800)米,若他想尽快到达出口A,根据s的大小,在等候乘1号车还是步行这两种方式中,他该如何选择?
(年四川内江12分)某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?