如图,在平面直角坐标系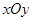 中,半径为1的圆的圆心
中,半径为1的圆的圆心 在坐标原点,且与两坐标轴分别交于
在坐标原点,且与两坐标轴分别交于 四点.抛物线
四点.抛物线 与
与 轴交于点
轴交于点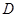 ,与直线
,与直线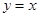 交于点
交于点 ,且
,且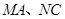 分别与圆
分别与圆 相切于点
相切于点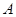 和点
和点 .
.
(1)求抛物线的解析式;
(2)抛物线的对称轴交 轴于点
轴于点 ,连结
,连结 ,并延长
,并延长 交圆
交圆 于
于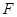 ,求
,求 的长.
的长.
(3)过点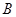 作圆
作圆 的切线交
的切线交 的延长线于点
的延长线于点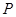 ,判断点
,判断点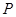 是否在抛物线上,说明理由.
是否在抛物线上,说明理由.
计算:
(1)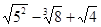
(2)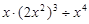
(3)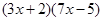
(4)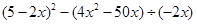
已知,如图,在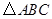 中,
中,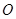 是高
是高 和
和 的交点,观察图形,试猜想
的交点,观察图形,试猜想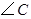 和
和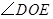 之间具有怎样的数量关系,并论证你的猜想.
之间具有怎样的数量关系,并论证你的猜想.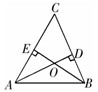
已知,如图,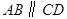 ,
,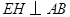 ,垂足为
,垂足为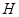 ,若
,若 ,则
,则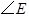 为多少度?
为多少度?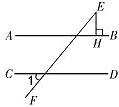
已知:如图,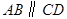 ,
, ,
,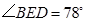 ,求
,求 的度数.
的度数.
某产品每件的成本是100元,为了解市场对该产品的认可规律,销售部门分别按两种方案组织了试销售,情况如下:
方案A:固定以每件140元的价格销售,日销售量为50件;
方案B:每天都适当调整售价,发现日销售量y(件)近似是售价x(元)的一次函数,且前三天的销售情况如下表所示:
| x(元) |
130 |
140 |
150 |
| y(件) |
70 |
50 |
30 |
如果方案B中的第四天的售价为155元、第五天的售价为160元,那么前五天中,哪种方案的销售总利润大?