有一种摸奖游戏，一个不透明的袋中装有大小相同的红球5个，白球10个，摸奖者每次随机地从袋中摸出5个球查看后再全部放回，若这5个球中有3个红球则中三等奖，有4个红球则中二等奖，有5个红球则中一等奖．
（1）某人摸奖一次，问他中奖的概率有多大？
（2）某人摸奖一次，若已知他中奖了，问他中二等奖的概率有多大？
如图，四边形ABCD是直角梯形，∠ABC＝∠BAD＝90°，SA⊥
平面ABCD， SA＝AB＝BC＝2，AD＝1．
（Ⅰ）求SC与平面ASD所成的角余弦；
（Ⅱ）求平面SAB和平面SCD所成角的余弦．
已知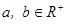
,试证：
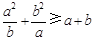；并求函数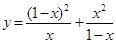
（
）的最小值.
已知
：
：
．
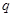（Ⅰ）若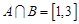
,求实数
的值；
（Ⅱ）若是
的充分条件，求实数的取值范围．
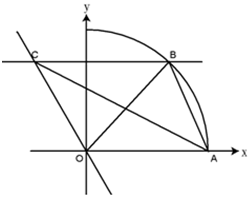
（本小题满分14分）在如图所示的直角坐标系中，
为单位圆在第一象限内圆弧上的动点，
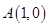，设
，过作直线
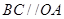，并交直线
于点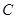
．
（Ⅰ）求点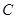的坐标 (用
表示) ；
（Ⅱ）判断
能否为
？若能，求出点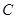的坐标，若不能，请说明理由．
(Ⅲ) 试求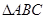
的面积的最大值，并求出相应
值．
（本小题满分12分）．对任意函数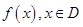
，可按右图构造一个数列发生器．记由数列发生器产生数列
．
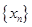（Ⅰ）若定义函数
，且输入
，请写出数列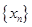的所有项；
（Ⅱ）若定义函数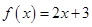
，且输入
，求数列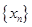的通项公式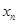
．
(Ⅲ)若定义函数
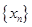，且要产生一个无穷的常数列，试求输入的初始数据
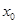的值及相应数列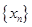的通项公式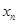．