已知数列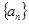 的前
的前 项和为
项和为 ,向量
,向量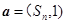 ,
, ,满足条件
,满足条件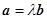 ,
, 且
且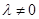 .
.
(1)求数列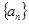 的通项公式;
的通项公式;
(2)设函数 ,数列
,数列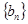 满足条件
满足条件 ,
,
①求数列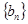 的通项公式;
的通项公式;
②设 ,求数列
,求数列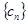 的前
的前 和
和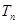 .
.
(本小题满分12分)某城市有东西南北四个进入城区主干道的入口,在早高峰时间段,时常发生交通拥堵现象,交警部门统计11月份30天内的拥堵天数,东西南北四个主干道入口的拥堵天数分别是18天,15天,9天,15天.假设每个入口发生拥堵现象互相独立,视频率为概率.
(1)求该城市一天中早高峰时间段恰有三个入口发生拥堵的概率;
(2)设 表示一天中早高峰时间段发生拥堵的主干道入口个数,求
表示一天中早高峰时间段发生拥堵的主干道入口个数,求 的分布列和数学期望.
的分布列和数学期望.
【改编】已知函数 ,
,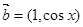
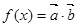
 R
R ,
, 是函数
是函数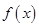 的一个零点.
的一个零点.
(1)求 的值,并求函数
的值,并求函数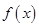 的对称轴及单调递增区间;
的对称轴及单调递增区间;
(2)若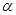
 ,且
,且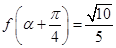 ,
, ,求
,求 的值.
的值.
(本小题满分14分)已知函数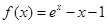 ,
,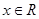 , 其中,
, 其中,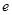 是自然对数的底数.函数
是自然对数的底数.函数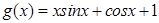 ,
,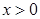 .
.
(Ⅰ)求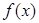 的最小值;
的最小值;
(Ⅱ)将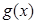 的全部零点按照从小到大的顺序排成数列
的全部零点按照从小到大的顺序排成数列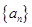 ,求证:
,求证:
(1)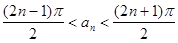 ,其中
,其中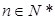 ;
;
(2)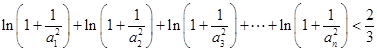 .
.
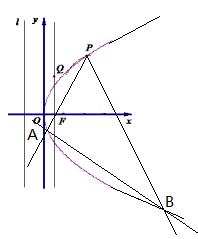
(本小题满分13分)如图,设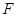 为抛物线
为抛物线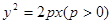 的焦点,
的焦点,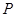 是抛物线上一定点,其
是抛物线上一定点,其
坐为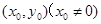 ,
,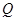 为线段
为线段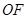 的垂直平分线上一点,且点
的垂直平分线上一点,且点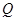 到抛物线的准线
到抛物线的准线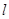 的距离为
的距离为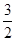 .
.
(Ⅰ)求抛物线的方程;
(Ⅱ)过点P任作两条斜率均存在的直线PA、PB,分别与抛物线交于点A、B,如图示,若直线AB的斜率为定值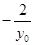 ,求证:直线PA、PB的倾斜角互补.
,求证:直线PA、PB的倾斜角互补.