为加强中学生实践、创新能力和团队精神的培养,促进教育教学改革,教育部门主办了全国中学生航模竞赛. 该竞赛分为预赛和决赛两个阶段,参加决赛的队伍按照抽签方式决定出场顺序.通过预赛,选拔出甲、乙、丙和丁四支队伍参加决赛.
(Ⅰ)求决赛中甲、乙两支队伍恰好排在前两位的概率;
⑾求决赛中甲、乙两支队伍出场顺序相邻的概率.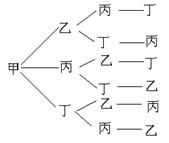
已知椭圆E的长轴的一个端点是抛物线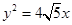 的焦点,离心率是
的焦点,离心率是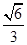 .
.
(1)求椭圆E的方程;
(2)过点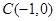 ,斜率为k的动直线与椭圆E相交于A、B两点,请问x轴上是否存在点M,使
,斜率为k的动直线与椭圆E相交于A、B两点,请问x轴上是否存在点M,使 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由.
已知函数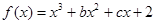
若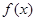 在
在 时有极值
时有极值 ,求
,求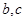 的值;
的值;
(2)在(1)的条件下,若函数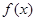 的图象与函数
的图象与函数 的图象恰有三个不同的交点,求实数
的图象恰有三个不同的交点,求实数 的取值范围.
的取值范围.
已知抛物线 (
( )的准线与
)的准线与 轴交于点
轴交于点 .
.
(1)求抛物线的方程,并写出焦点坐标;
(2)是否存在过焦点的直线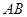 (直线与抛物线交于点
(直线与抛物线交于点 ,
, ),使得三角形
),使得三角形 的面积
的面积 ?若存在,请求出直线
?若存在,请求出直线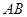 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:,,… ,后得到如图的频率分布直方图.
(1)求图中实数 的值;
的值;
(2)若该校高一年级共有学生500人,试估计该校高一年级在这次考试中成绩不低于60分的人数.
(3)若从样本中数学成绩在与两个分数段内的学生中随机选取两名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.
已知 :
: ,
, :函数
:函数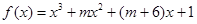 存在极大值和极小值,求使“
存在极大值和极小值,求使“ ”为真命题的实数
”为真命题的实数 的取值范围.
的取值范围.