某城市现有人口总数为100万人,如果年自然增长率为1.2%,试解答下列问题:
⑴写出该城市人口数y(万人)与年份x(年)的函数关系式;
⑵用程序表示计算10年以后该城市人口总数的算法;
⑶用程序表示如下算法:计算大约多少年以后该城市人口将达到120万人.
为了调查胃病是否与生活规律有关,在某地对 名
名 岁以上的人进行了调查,结果是:患胃病者生活不规律的共
岁以上的人进行了调查,结果是:患胃病者生活不规律的共 人,患胃病者生活规律的共
人,患胃病者生活规律的共 人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共
人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共 人.
人.
(1)根据以上数据列出 列联表.
列联表.
(2)并判断 岁以上的人患胃病与否和生活规律是否有关。
岁以上的人患胃病与否和生活规律是否有关。
已知复数 .
.
(Ⅰ)当实数 取什么值时,复数
取什么值时,复数 是:①实数; ②虚数;③纯虚数;
是:①实数; ②虚数;③纯虚数;
(Ⅱ)在复平面内,若复数 所对应的点在第二象限,求
所对应的点在第二象限,求 的取值范围.
的取值范围.
一家新技术公司计划研制一个名片管理系统,希望系统能够具备以下功能:
(1)用户管理:能修改密码,显示用户信息,修改用户信息。
(2)用户登录。
(3)名片管理:能够对名片进行删除、添加、修改、查询。
(4)出错信息处理。
请根据这些要求画出该系统的结构图.
设 ,
,
(1)当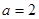 时,求曲线
时,求曲线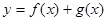 在
在 处的切线方程
处的切线方程
(2)如果对任意的 ,恒有
,恒有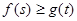 成立,求实数
成立,求实数 的取值范围
的取值范围
(1) ,
, 则
则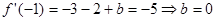
(2)由(1)知 ,则
,则
①当 时,
时, ,令
,令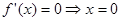 或
或
 ,
,
 在
在 上的值域为
上的值域为
② 当 时, a.若
时, a.若 ,则
,则
b.若 ,则
,则 在
在 上是单调减的
上是单调减的
 在
在 上的值域为
上的值域为
c.若 则
则 在
在 上是单调增的
上是单调增的
 在
在 上的值域为
上的值域为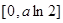
综上所述,当 时,
时, 在
在 的值域为
的值域为
当 时,
时, 在
在 的值域为
的值域为
当 时,若
时,若

 时,
时, 在
在 的值域为
的值域为
若

 时,
时, 在
在 的值域为
的值域为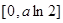
即当 时,
时, 在
在 的值域为
的值域为
当 时,
时, 在
在 的值域为
的值域为
当 时,
时, 在
在 的值域为
的值域为