求过点A(2,1),且与直线2x+y-10=0垂直的直线方程、
已知函数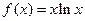 .(Ⅰ)求
.(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)当 时,求证:
时,求证: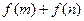 ≥
≥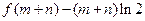 .
.
已知椭圆C: 的离心率为
的离心率为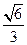 ,过右焦点F且斜率为1的直线交椭圆C于A、B两点,N为弦AB的中点.
,过右焦点F且斜率为1的直线交椭圆C于A、B两点,N为弦AB的中点.
(Ⅰ)求直线ON(O为坐标原点)的斜率 ;
;
(Ⅱ)对于椭圆C上任意一点M,试证:对任意的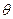
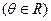 等式
等式 都成立.
都成立.
某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为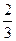 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为
(I)求徒弟加工2个零件都是精品的概率;
(II)求徒弟加工该零件的精品数多于师父的概率;
(III)设师徒二人加工出的4个零件中精品个数为 ,求
,求 的分布列与均值E
的分布列与均值E .
.
如图1所示,在边长为12的正方形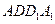 中,点
中,点 在线段
在线段 上,且
上,且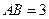 ,
, ,作
,作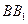
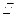
 ,分别交
,分别交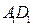 ,
, 于点
于点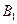 ,
,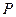 ,作
,作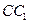
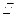
 ,分别交
,分别交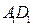 ,
, 于点
于点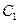 ,
, ,将该正方形沿
,将该正方形沿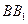 ,
,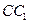 折叠,使得
折叠,使得 与
与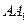 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱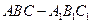 .
.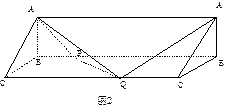
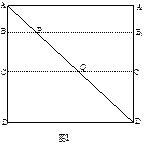
(Ⅰ)求证: 平面
平面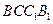 ;
;
(Ⅱ)求四棱锥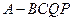 的体积;
的体积;
(Ⅲ)求平面 与平面
与平面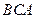 所成锐二面角的余弦值.
所成锐二面角的余弦值.
设函数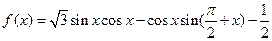 .
.
(Ⅰ)求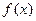 的最小正周期;
的最小正周期;
(Ⅱ)当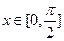 时,求函数
时,求函数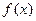 的最大值和最小值.
的最大值和最小值.