如图1所示,在边长为12的正方形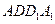 中,点
中,点 在线段
在线段 上,且
上,且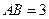 ,
, ,作
,作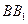
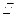
 ,分别交
,分别交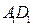 ,
, 于点
于点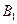 ,
,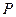 ,作
,作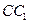
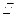
 ,分别交
,分别交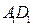 ,
, 于点
于点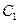 ,
, ,将该正方形沿
,将该正方形沿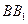 ,
,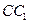 折叠,使得
折叠,使得 与
与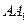 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱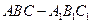 .
.
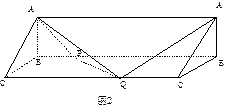
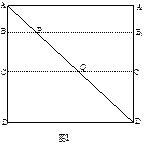
(Ⅰ)求证: 平面
平面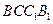 ;
;
(Ⅱ)求四棱锥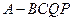 的体积;
的体积;
(Ⅲ)求平面 与平面
与平面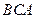 所成锐二面角的余弦值.
所成锐二面角的余弦值.
给定椭圆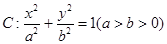 .称圆心在原点O,半径为
.称圆心在原点O,半径为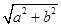 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为 .
.
(1)求椭圆C的方程和其“准圆”方程;
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线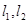 ,使得
,使得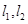 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断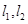 是否垂直?并说明理由.
是否垂直?并说明理由.
已知函数 , 数列
, 数列 满足
满足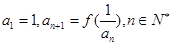 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令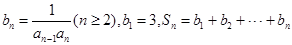 ,若
,若 对一切
对一切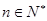 成立,求最小正整数m.
成立,求最小正整数m.
如图,已知正方体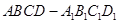 的棱长为2,E、F分别是
的棱长为2,E、F分别是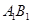 、
、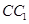 的中点,过
的中点,过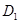 、E、F作平面
、E、F作平面 交
交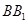 于G.
于G.
(l)求证:EG∥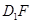 ;
;
(2)求二面角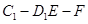 的余弦值;
的余弦值;
(3)求正方体被平面 所截得的几何体
所截得的几何体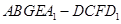 的体积.
的体积.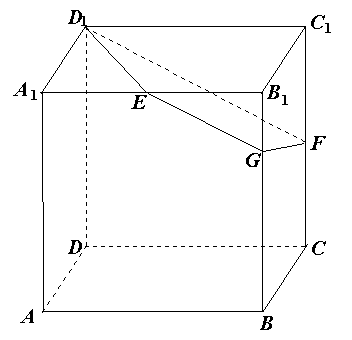
下图是某市3月1日至14日空气质量指数趋势图,空气质量指数小于1 00表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1曰至3月1 3日中某一天到达该市,并停留2天.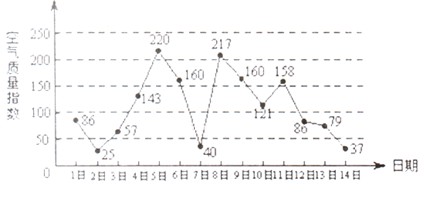
(l)求此人到达当日空气重度污染的概率;
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望。
已知函数,
(l)求函数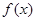 的最小正周期;
的最小正周期;
(2)当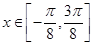 时,求函数f(x)的单调区间。
时,求函数f(x)的单调区间。