下图是某市3月1日至14日空气质量指数趋势图,空气质量指数小于1 00表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1曰至3月1 3日中某一天到达该市,并停留2天.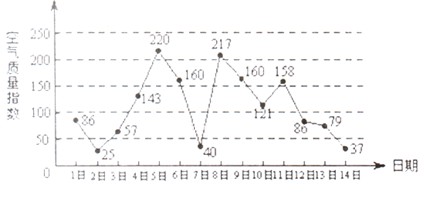
(l)求此人到达当日空气重度污染的概率;
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望。
已知集合A={x|x2-4x-5≤0},
B={x|x2-2x-m<0}.
(1)当m=3时,求A∩∁RB;
(2)若A∩B={x|-1≤x<4},求实数m的值
判断下列命题的真假.
(1)命题“在△ABC中,若AB>AC,则∠C>∠B”的逆命题;
(2)命题“若ab≠0,则a≠0且b≠0”的否命题;
(3)命题“若a≠0,且b≠0,则ab≠0”的逆否命题
对于数列 :
: ,若满足
,若满足 ,则称数列
,则称数列 为“0-1
为“0-1
数列”.定义变换 ,
, 将“0-1数列”
将“0-1数列” 中原有的每个1都变成0,1,原有的每个0都变成1,0。例如
中原有的每个1都变成0,1,原有的每个0都变成1,0。例如 :1,0,1,则
:1,0,1,则 :
: 设
设 是“0-1数列”,令
是“0-1数列”,令 ,
,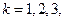 …。
…。
(1)若数列 :
: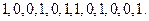 求数列
求数列 ;
;
(2)若数列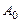 共有10项,则数列
共有10项,则数列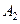 中连续两项
中连续两项 相等的数对至少有多少对?请说明理由;
相等的数对至少有多少对?请说明理由;
(3)若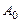 为0,1,记数列
为0,1,记数列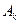 中连续两项都是0的数对
中连续两项都是0的数对 个数为
个数为 ,
,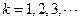 ,
,
求 关于
关于 的表达式
的表达式
设幂函数 ,记
,记 。
。
(1)若 ,求
,求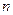 的值;
的值;
(2)证明: ;
;
(3)对于任意的a、b、 c
c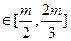 ,问以
,问以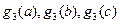 的值为长的三条线段是否可构成三角形?请说明理由。
的值为长的三条线段是否可构成三角形?请说明理由。
已知 、
、 分别是椭圆
分别是椭圆 的左、右焦点,点B是其上顶点,椭圆的右准线与
的左、右焦点,点B是其上顶点,椭圆的右准线与
 轴交于点N,且
轴交于点N,且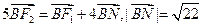 。
。
(1)求椭圆方程;
(2)直线 :
: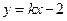 与椭圆交于不同的两点M、Q,若△BMQ是以MQ为底边的等腰三角形,求
与椭圆交于不同的两点M、Q,若△BMQ是以MQ为底边的等腰三角形,求 的值。
的值。