在平面直角坐标系中,已知向量 (
(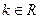 ),
), ,动点
,动点 的轨迹为T.
的轨迹为T.
(1)求轨迹T的方程,并说明该方程表示的曲线的形状;
(2)当 时,已知
时,已知 、
、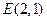 ,试探究是否存在这样的点
,试探究是否存在这样的点 :
: 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积 ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.
已知函数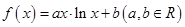 ,在点
,在点 处的切线方程是
处的切线方程是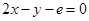 (e为自然对数的底)。
(e为自然对数的底)。
(1)求实数 的值及
的值及 的解析式;
的解析式;
(2)若 是正数,设
是正数,设 ,求
,求 的最小值;
的最小值;
(3)若关于x的不等式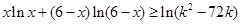 对一切
对一切 恒成立,求实数
恒成立,求实数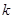 的取值范围。
的取值范围。
若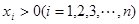 ,观察下列不等式:
,观察下列不等式: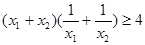 ,
, ,…,请你猜测
,…,请你猜测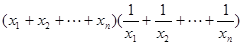 将满足的不等式,并用数学归纳法加以证明。
将满足的不等式,并用数学归纳法加以证明。
如图,点 为斜三棱柱
为斜三棱柱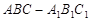 的侧棱
的侧棱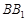 上一点,
上一点,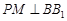 交
交 于点
于点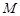 ,
,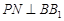 交
交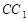 于点
于点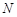 .
.
(1) 求证: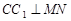 ;
;
(2) 在任意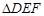 中有余弦定理:
中有余弦定理: .
.
拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明
已知二次函数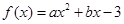 在
在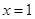 处取得极值,且在
处取得极值,且在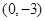 点处的切线与直线
点处的切线与直线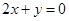 平行.
平行.
(1)求 的解析式;
的解析式;
(2)求函数 的单调递增区间及极值。
的单调递增区间及极值。
(3)求函数 在
在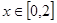 的最值。
的最值。
有9本不同的课外书,分给甲、乙、丙三名同学,求在下列条件下,各有多少种分法?
(1)甲得4本,乙得3本,丙得2本;
(2)一人得4本,一人得3本,一人得2本;
(3)甲、乙、丙各得3本.